题目内容
设复数z=cosθ+isinθ，θ∈[0，π]，ω=-1+i，则|z-ω|的最大值是（ ）A．
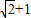
B．
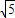
C．
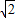
D．
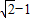
【答案】分析：利用复数的减法代入后整理，然后运用求模公式写出|z-ω|的模，最后利用三角函数的化简进行求值．
解答：解：由z=cosθ+isinθ，θ∈[0，π]，ω=-1+i，得：z-ω=cosθ+isinθ-（-1+i）=（cosθ+1）+（sinθ-1）i，
所以|z-ω|=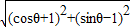
=
=
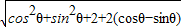
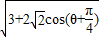，因为θ∈[0，π]，所以
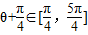，所以
所以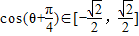|z-ω|的最大值是
．
故选B．
点评：本题考查了复数的模，考查了三角函数的化简与求值，考查了学生的运算能力，此题是中档题．
解答：解：由z=cosθ+isinθ，θ∈[0，π]，ω=-1+i，得：z-ω=cosθ+isinθ-（-1+i）=（cosθ+1）+（sinθ-1）i，
所以|z-ω|=
==
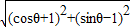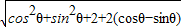
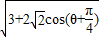，因为θ∈[0，π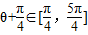]，所以，所以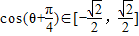所以|z-ω|的最大值是
．故选B．
点评：本题考查了复数的模，考查了三角函数的化简与求值，考查了学生的运算能力，此题是中档题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
设复数z=cosθ+icosθ，θ∈[0，π]，ω=-1+i，则|z-ω|的最大值是（ ）
A、
| ||
B、
| ||
| C、2 | ||
D、
|