题目内容
已知平面内任一点O满足
=x
+y
(x,y∈R),则“x+y=1”是“点P在直线AB上”的( )
| OP |
| OA |
| OB |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
分析:将三点共线等价于以此三点为起点、终点的两个向量共线,利用向量的运算法则,将两个向量用以O为起点的向量表示,得到x、y的关系.
解答:解:“点P在直线AB上”的充要条件为
=λ
即
-
=λ(
-
)
即
=(1+λ)
+λ
∵
=x
+y
(x,y∈R)
∴
∴x+y=1
“x+y=1”是“点P在直线AB上”的充要条件
故选C.
| AP |
| AB |
即
| OP |
| OA |
| OB |
| OA |
即
| OP |
| OA |
| OB |
∵
| OP |
| OA |
| OB |
∴
|
∴x+y=1
“x+y=1”是“点P在直线AB上”的充要条件
故选C.
点评:解决三点共线问题常转化为以此三点为起点、终点的两个向量共线,再利用向量共线的充要条件解决.

练习册系列答案
相关题目
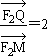 ,求点
,求点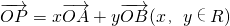 ,则“x+y=1”是“点P在直线AB上”的
,则“x+y=1”是“点P在直线AB上”的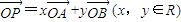 ,则“x+y=1”是“点P在直线AB上”的( )
,则“x+y=1”是“点P在直线AB上”的( )