题目内容
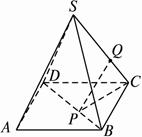
 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.(1)求证:直线SA∥平面BDE;
(2)求二面角A-SB-D的余弦值;
(3)求直线BD和平面SBC所成角的正弦值.
分析:(1)欲证直线SA∥平面BDE,根据直线与平面平行的判定定理可知只需证SA与平面BDE内一直线平行,连接AC交BD于点O,连接OE,根据中位线可知SA∥OE,又OE?平面BDE,SA?平面BDE,满足定理所需条件;
(2)连接SO,取SB中点F,连接AF、OF,SB⊥AF,根据三垂线定理的逆定理,得OF⊥SB,从而∠AFO是二面角A-SB-D的平面角.在AOF中,求出此角的余弦值即可;
(3)过D作平面SBC的垂线,垂足在交线BE上,根据线面所成角的定义可知∠DBE为直线BD和平面SBC所成的角,然后在三角形DBE中求出线BD和平面SBC所成的角的正弦值的即可.
(2)连接SO,取SB中点F,连接AF、OF,SB⊥AF,根据三垂线定理的逆定理,得OF⊥SB,从而∠AFO是二面角A-SB-D的平面角.在AOF中,求出此角的余弦值即可;
(3)过D作平面SBC的垂线,垂足在交线BE上,根据线面所成角的定义可知∠DBE为直线BD和平面SBC所成的角,然后在三角形DBE中求出线BD和平面SBC所成的角的正弦值的即可.
解答: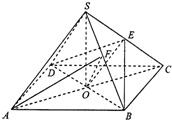 (1)证明:连接AC交BD于点O,连接OE,
(1)证明:连接AC交BD于点O,连接OE,
∵S-ABCD是正四棱锥,
∴ABCD是正方形,∴O是AC的中点.
∵E是侧棱SC的中点,∴SA∥OE,
又OE?平面BDE,SA?平面BDE,
∴直线SA∥平面BDE.(4分)
(2)解:∵AD∥BC,
∴∠SAD=60°为异面直线SA和BC所成的角,△SAD是等边三角形.
根据正棱锥的性质得,△SCD、△SAB、△SBC也是等边三角形.
连接SO,取SB中点F,连接AF、OF,
∵O是正方形ABCD的中心,根据正棱锥的性质得,SO⊥平面ABCD,
∴AO⊥SO,又AO⊥BD,∴AO⊥平面SBD.
∵SB⊥AF,根据三垂线定理的逆定理,得OF⊥SB,
∴∠AFO是二面角A-SB-D的平面角.AOF中,OF=
SD,AF=
SA=
SD,cos∠AFO=
=
,
∴二面角A-SB-D的余弦值是
.(9分)
(3)解:∵E是侧棱SC的中点,∴BE⊥SC,DE⊥SC,∴SC⊥平面BDE,
∴平面SBC⊥平面BDE,过D作平面SBC的垂线,垂足在交线BE上,
即BE为BD在平面SBC上的射影,∴∠DBE为直线BD和平面SBC所成的角,
∵OE=
SA,BE=
SB=
SA,
∴sin∠DBE=sin∠OBE=
=
,
∴线BD和平面SBC所成的角的正弦值为
.(14分)
 (1)证明:连接AC交BD于点O,连接OE,
(1)证明:连接AC交BD于点O,连接OE,∵S-ABCD是正四棱锥,
∴ABCD是正方形,∴O是AC的中点.
∵E是侧棱SC的中点,∴SA∥OE,
又OE?平面BDE,SA?平面BDE,
∴直线SA∥平面BDE.(4分)
(2)解:∵AD∥BC,
∴∠SAD=60°为异面直线SA和BC所成的角,△SAD是等边三角形.
根据正棱锥的性质得,△SCD、△SAB、△SBC也是等边三角形.
连接SO,取SB中点F,连接AF、OF,
∵O是正方形ABCD的中心,根据正棱锥的性质得,SO⊥平面ABCD,
∴AO⊥SO,又AO⊥BD,∴AO⊥平面SBD.
∵SB⊥AF,根据三垂线定理的逆定理,得OF⊥SB,
∴∠AFO是二面角A-SB-D的平面角.AOF中,OF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| OF |
| AF |
| ||
| 3 |
∴二面角A-SB-D的余弦值是
| ||
| 3 |
(3)解:∵E是侧棱SC的中点,∴BE⊥SC,DE⊥SC,∴SC⊥平面BDE,
∴平面SBC⊥平面BDE,过D作平面SBC的垂线,垂足在交线BE上,
即BE为BD在平面SBC上的射影,∴∠DBE为直线BD和平面SBC所成的角,
∵OE=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴sin∠DBE=sin∠OBE=
| OE |
| BE |
| ||
| 3 |
∴线BD和平面SBC所成的角的正弦值为
| ||
| 3 |
点评:本题综合考查空间中线线、线面的位置关系和空间中角的计算,涉及线线角、线面角和二面角的平面角,传统方法和坐标向量法均可,考查的知识面较广,难度中等,值得一做.

练习册系列答案
相关题目
 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )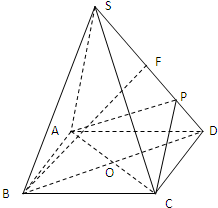 如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的
如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的 (2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的
(2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的