题目内容
(2007
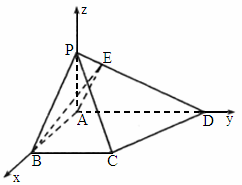
北京宣武模拟)如下图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.(1)
若AE⊥PD,E为垂足,求证:BE⊥PD;(2)
在(1)的条件下,求异面直线AE与CD所成角的余弦值;(3)
求平面PAB与平面PCD所成的二面角的正切值.
答案:略
解析:
解析:
|
解析: (1)如图建立空间直角坐标系,
则 A(0,0,0),B(a,0,0),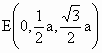 ,C(a,a,0),D(0,2a,0), ,C(a,a,0),D(0,2a,0),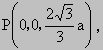
∴ 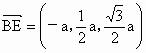 , ,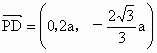 , ,
∴ 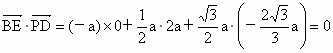 ,∴BE⊥PD. ,∴BE⊥PD.
则 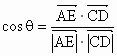 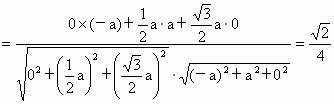 , ,
∴异面直线 AE与CD所成角的余弦值为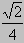 . .
(3) 易知,CB⊥AB,CB⊥PA.则 CB⊥平面PAB.
又设平面 PCD的一个法向量为m=(x ,y,z),则 m⊥PC,m⊥CD.
∴由 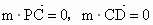 , ,
得 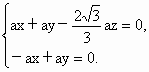 ∴ ∴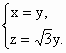
则 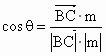 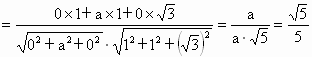 .∴tanθ=2. .∴tanθ=2.
∴平面 PAB与平面PCD所成二面角的正切值为2. |

练习册系列答案
相关题目
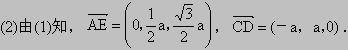
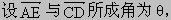

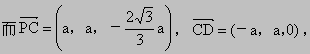
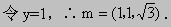

 分别是双曲线
分别是双曲线 的左、右焦点,P为双曲线左支上任意一点,若
的左、右焦点,P为双曲线左支上任意一点,若 的最小值为8a,则该双曲线离心率e的取值范围是________.
的最小值为8a,则该双曲线离心率e的取值范围是________. R),其中[x]表示不超过x的最大整数.
R),其中[x]表示不超过x的最大整数.
 ,f(x)的值域为
,f(x)的值域为 ,现将
,现将 ,试求
,试求 与
与 表示等差数列
表示等差数列 的前n项和,且
的前n项和,且 若
若 ,则n=________.
,则n=________. ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 .)
.)
