题目内容
(本小题满分12分)
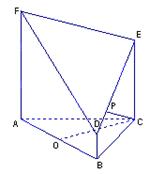
如图所示的几何体是由以正三角形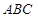 为底面的直棱柱
为底面的直棱柱
被平面 所截而得.
所截而得. 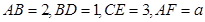 ,
,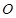 为
为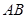 的中点.
的中点.
(Ⅰ)当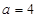 时,求平面
时,求平面 与平面
与平面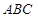 的夹角的余弦值;
的夹角的余弦值;
(Ⅱ)当 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使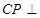 平面
平面 ?
?
【答案】
(1)分别取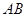 、
、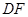 的中点
的中点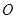 、
、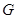 ,连接
,连接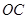 、
、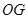 .
.
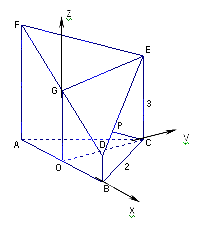
以直线 、
、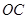 、
、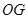 分别为
分别为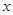 轴、
轴、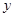 轴、
轴、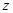 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,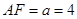 ,则
,则 、
、 、
、 的坐标分别为
的坐标分别为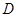 (1,0,1)、
(1,0,1)、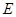 (0,
(0,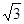 ,3)、
,3)、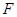 (-1,0,4),
(-1,0,4),
∴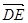 =(-1,
=(-1,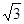 ,2),
,2),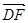 =(-2,0,3)
=(-2,0,3)
设平面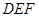 的法向量
的法向量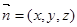 ,
,
由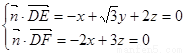 得
得
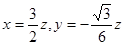 ,可取
,可取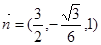
平面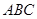 的法向量可以取
的法向量可以取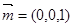
∴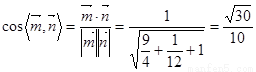
∴平面 与平面
与平面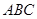 的夹角的余弦值为
的夹角的余弦值为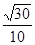 .
.
(2)在(1)的坐标系中,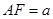 ,
,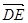 =(-1,
=(-1,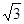 ,2),
,2),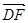 =(-2,0,
=(-2,0,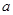 -1).
-1).
因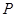 在
在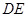 上,设
上,设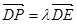 ,则
,则
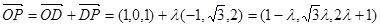
∴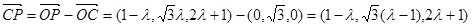
于是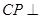 平面
平面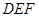 的充要条件为
的充要条件为
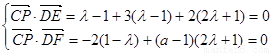
由此解得,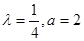
即当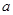 =2时,在
=2时,在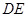 上存在靠近
上存在靠近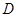 的第一个四等分点
的第一个四等分点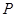 ,使
,使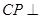 平面
平面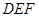 .
.
【解析】略

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目