题目内容
函数f(x)=1g
(x≠0,x∈R),有下列命题:
①f(x)的图象关于y轴对称;
②f(x)的最小值是2;
③f(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数;
④f(x)没有最大值.
其中正确命题的序号是
| x2+1 | |x| |
①f(x)的图象关于y轴对称;
②f(x)的最小值是2;
③f(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数;
④f(x)没有最大值.
其中正确命题的序号是
①④
①④
.(请填上所有正确命题的序号)分析:①f(-x)=1g
=f(x),函数f(x)是偶函数;
②利用基本不等式,可得
=|x|+
≥2,从而f(x)=1g
≥lg2;
③考查函数g(x)=
=|x|+
的单调性,即可得到结论;
④由③知,f(x)没有最大值.
| x2+1 |
| |x| |
②利用基本不等式,可得
| x2+1 |
| |x| |
| 1 |
| |x| |
| x2+1 |
| |x| |
③考查函数g(x)=
| x2+1 |
| |x| |
| 1 |
| |x| |
④由③知,f(x)没有最大值.
解答:解:①f(-x)=1g
=f(x),∴函数f(x)是偶函数,f(x)的图象关于y轴对称,故①正确;
②
=|x|+
≥2,∴f(x)=1g
≥lg2,∴f(x)的最小值是lg2,故②不正确;
③函数g(x)=
=|x|+
在(-∞,-1),(0,1)上是减函数,在(-1,0),(1,+∞)上是增函数,故函数f(x)=1g
在(-∞,-1),(0,1)上是减函数,在(-1,0),(1,+∞)上是增函数,故③不正确;
④由③知,f(x)没有最大值,故④正确
故答案为:①④
| x2+1 |
| |x| |
②
| x2+1 |
| |x| |
| 1 |
| |x| |
| x2+1 |
| |x| |
③函数g(x)=
| x2+1 |
| |x| |
| 1 |
| |x| |
| x2+1 |
| |x| |
④由③知,f(x)没有最大值,故④正确
故答案为:①④
点评:本题考查命题的真假判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
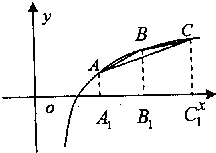 在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).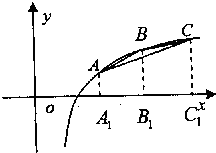 在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).