题目内容
已知函数
(Ⅰ)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)在 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值.

(Ⅰ)求函数
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;(Ⅱ)在
 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值.(1) ,
, 的单调递增区间为
的单调递增区间为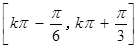 (
(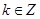 ).
).
(2)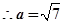
 ,
, 的单调递增区间为
的单调递增区间为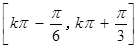 (
(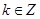 ).
). (2)
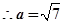
试题分析:解:(Ⅰ)
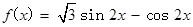 2分
2分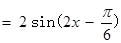 4分
4分 5分
5分由
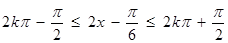 得,
得,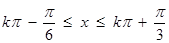 (
(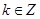 )., 7分
)., 7分故
 的单调递增区间为
的单调递增区间为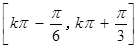 (
(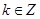 ). 8分
). 8分(Ⅱ)
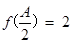 ,则
,则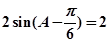
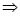
 9分
9分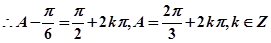 10分
10分又
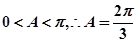 11分
11分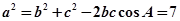 12分
12分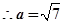 13分
13分点评:解决的关键是利用二倍角公式将表达式化为单一函数,同时能结合性质来得到结论,属于基础题。

练习册系列答案
相关题目
 ,
, .
. 的表达式;
的表达式; 和函数
和函数 的图象关于原点对称,
的图象关于原点对称, 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.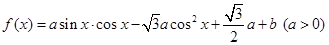
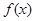 的最小正周期;
的最小正周期;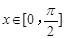 ,
,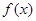 的最小值是
的最小值是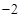 ,最大值是
,最大值是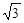 ,求实数
,求实数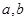 的值.
的值.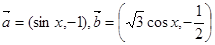 ,函数
,函数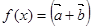 ·
·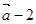
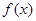 的最小正周期T及单调减区间
的最小正周期T及单调减区间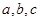 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角,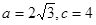 且
且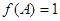 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S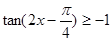 的解集是________。
的解集是________。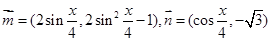 ,函数
,函数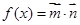 .
.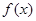 的最大值,并写出相应
的最大值,并写出相应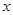 的取值集合;
的取值集合;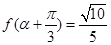 ,且
,且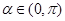 ,求
,求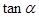 的值.
的值.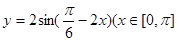 )为增函数的区间是( )
)为增函数的区间是( )



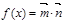 其中
其中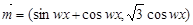 ,
,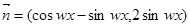
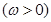 ,若
,若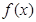 图象中相邻的两条对称轴间的距离不小于
图象中相邻的两条对称轴间的距离不小于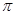 。
。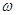 的取值范围
的取值范围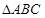 中,a,b,c分别为角A,B,C的对边,
中,a,b,c分别为角A,B,C的对边,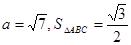 。当
。当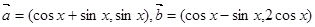 ,设
,设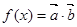 .
.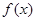 的最小正周期,并写出
的最小正周期,并写出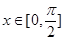 时,求函数
时,求函数