题目内容
当k为何值时，直线y=kx+k-2与抛物线y2=4x有两个公共点,仅有一个公共点,无公共点？
思路解析：可以考虑数形结合,也可以看方程组解的个数. 解：由方程组 （1）当k=0时，直线y=-2与抛物线y2=4x仅有一个公共点. （2）当k≠0时，Δ=4(k2-2k-2)2-4k2(k-2)2=-16(k2-2k-1). 当k∈（1- 当k=1± 当k∈（-∞，1- 综合以上情况，当k∈（1-
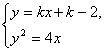消去y,得k2x2+2(k2-2k-2)+(k-2)2=0.
，0）∪（0，1+
）时，Δ＞0，直线与抛物线有两个公共点；
时，Δ=0，直线与抛物线仅有一个公共点；
）∪（1+
，+∞）时，Δ＜0，直线与抛物线没有公共点.
，0）∪（0，1+
）时，直线与抛物线有两个公共点;当k=0或k=1±
时，直线与抛物线仅有一个公共点;当k∈（-∞，1-
）∪（1+
，+∞）时，直线与抛物线没有公共点.
练习册系列答案
新教材新学案系列答案
金版课堂名师导学案系列答案
一线调研单元评估卷今年新试卷系列答案
全效课堂新课程精讲细练系列答案
首席课时训练系列答案
一天一练系列答案
一线调研今年新试卷系列答案
相关题目
＋y2＝1①有两个公共点；②有一个公共点；③没有公共点．
(
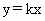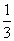＜k＜3)分四边形OABC为两部分，S表示靠近x轴一
(
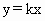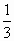＜k＜3)分四边形OABC为两部分，S表示靠近x轴一