题目内容
四边形
OABC的四个顶点坐标分别为O(0,0)、A(6,2)、B(4,6)、C(2,6),直线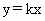 (
(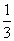 <k<3)分四边形OABC为两部分,S表示靠近x轴一
<k<3)分四边形OABC为两部分,S表示靠近x轴一
侧的那一部分的面积.
(1)
求S=f(k)的函数表达式;(2)
当k为何值时,直线y=kx将四边形OABC分为面积相等的两部分.
答案:略
解析:
解析:
|
(1) 因为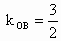 ,所以需分两种情况: ,所以需分两种情况:
①当 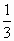 <k< <k<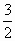 时,直线y=kx与AB:2x+y=14相交. 时,直线y=kx与AB:2x+y=14相交.
由 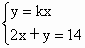 得交点 得交点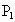 ( (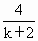 , ,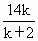 ) )
又点 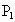 到直线OA:x-3y=0的距离为 到直线OA:x-3y=0的距离为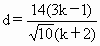
∴ 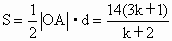 ; ;
②当 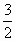 ≤k<3时,直线y=kx与BC:y=6交于 ≤k<3时,直线y=kx与BC:y=6交于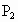 ( (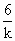 ,6) ,6)
∴ 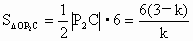
又 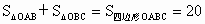
∴ 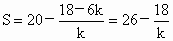 . .
故 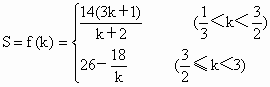
(2) 若直线y=kx平分四边形OABC的面积,由(1) 知,只须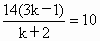 , ,
解得 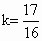 . . |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
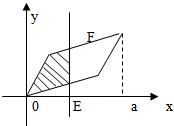 5、如图,垂直于x轴的直线EF经坐标原点向右平行移动,E是EF与x轴的交点,设OE=x(0≤x≤a),EF在扫平行四边形OABC的面积为y(阴影部分).则y=f(x)的大致图象是( )
5、如图,垂直于x轴的直线EF经坐标原点向右平行移动,E是EF与x轴的交点,设OE=x(0≤x≤a),EF在扫平行四边形OABC的面积为y(阴影部分).则y=f(x)的大致图象是( )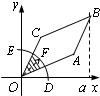 8、如图,圆弧型声波DFE从坐标原点O向外传播.若D是DFE弧与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )
8、如图,圆弧型声波DFE从坐标原点O向外传播.若D是DFE弧与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( ) 如图,垂直于x轴的直线EF经坐标原点O向右移动.若E是EF与x 轴的交点,设OE=x(0≤x≤a),EF在移动过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )
如图,垂直于x轴的直线EF经坐标原点O向右移动.若E是EF与x 轴的交点,设OE=x(0≤x≤a),EF在移动过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )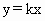 (
(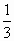 <k<3)分四边形OABC为两部分,S表示靠近x轴一
<k<3)分四边形OABC为两部分,S表示靠近x轴一