题目内容
设数列{an} 对任意n∈N*和实数常数,有| an-2an+1 |
| anan+1 |
| 1 |
| 3 |
(1)若{
| 1-an |
| an |
(2)设{bn}满足bn=(1-an)an,其前n项和Tn,求证:Tn>
| 2 |
| 3 |
| 2n-1 |
| 2n+1+1 |
分析:(1)由题设知
-1=2(
-1) +t•
-1=2,再由{
}是等比数列,得an=
.
(2)由bn=(1-an)an得bn=(1-
) •
=
<
-
,由此入手能够进行证明.
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| a1 |
| 1-an |
| an |
| 1 |
| 2n+1 |
(2)由bn=(1-an)an得bn=(1-
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n |
| (2n+1)2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1+1 |
解答:解:(1)由
=t-2,t∈R,a1=
,
得
-1=2(
-1) +t•
-1=2,
∵{
}是等比数列,
∴
-1=2n,
得an=
.
(2)由bn=(1-an)an得bn=(1-
) •
=
<
-
,
前n项和Tn=b1+b2+…+bn
<
-
=
•
.
| an-2an+1 |
| anan+1 |
| 1 |
| 3 |
得
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| a1 |
∵{
| 1-an |
| an |
∴
| 1 |
| an |
得an=
| 1 |
| 2n+1 |
(2)由bn=(1-an)an得bn=(1-
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n |
| (2n+1)2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1+1 |
前n项和Tn=b1+b2+…+bn
<
| 1 |
| 3 |
| 1 |
| 2n+1+1 |
=
| 2 |
| 3 |
| 2n-1 |
| 2n+1+1 |
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意合理地选取公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
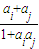 的值添在A的最后,然后删除ai,aj,这样得到一系列n-1项的新数列A1 (约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2,如此经过k次操作后得到的新数列记作Ak.设A:
的值添在A的最后,然后删除ai,aj,这样得到一系列n-1项的新数列A1 (约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2,如此经过k次操作后得到的新数列记作Ak.设A: ,则A3的可能结果是( )
,则A3的可能结果是( )

