题目内容
已知有穷数列A:a1,a2,…,an(n≥2,n∈N).定义如下操作过程T:从A中任取两项ai,aj,将
的值添在A的最后,然后删除ai,aj,这样得到一系列n-1项的新数列A1 (约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2,如此经过k次操作后得到的新数列记作Ak.设A:-
,
,
,
,则A3的可能结果是( )
| ai+aj |
| 1+aiaj |
| 5 |
| 7 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
分析:因为是单选题,可用排除法,逐一试验.
解答:解:因4数中
,
最简单,可先试这两个数,
=
,则数列A1为-
,
,
.又由于-
和
之和为0,故计算
=0,则A2为
,0.计算
=
,有此选项.
故选B
| 1 |
| 2 |
| 1 |
| 3 |
| ||||
1+
|
| 5 |
| 7 |
| 5 |
| 7 |
| 3 |
| 4 |
| 5 |
| 7 |
| 5 |
| 7 |
| 5 |
| 7 |
-
| ||||
1-
|
| 3 |
| 4 |
| ||
1+
|
| 3 |
| 4 |
故选B
点评:本题考查数列的概念,解题时要认真审题,仔细解答,避免错误.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 数列.对于
数列.对于 的值添在A的最后,然后删除ai,aj,这样得到一个n-1项的新数列A1(约定:一个数也视作数列)。若A1还是Γ数列,可继续实施操作过程T,得到的新数列记作A2,…,如此经过k次操作后得到的新数列记作Ak,
的值添在A的最后,然后删除ai,aj,这样得到一个n-1项的新数列A1(约定:一个数也视作数列)。若A1还是Γ数列,可继续实施操作过程T,得到的新数列记作A2,…,如此经过k次操作后得到的新数列记作Ak, ,请写出A1的所有可能的结果;
,请写出A1的所有可能的结果; ,求A9的可能结果,并说明理由.
,求A9的可能结果,并说明理由. 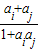 的值添在A的最后,然后删除ai,aj,这样得到一个n-1项的新数列A1(约定:一个数也视作数列).若A1还是
的值添在A的最后,然后删除ai,aj,这样得到一个n-1项的新数列A1(约定:一个数也视作数列).若A1还是 ,
, …请写出A1的所有可能的结果;
…请写出A1的所有可能的结果; ,-
,- ,-
,- ,-
,- ,
, ,
, ,
, ,
, ,
, ,
, …求A9的可能结果,并说明理由.
…求A9的可能结果,并说明理由.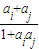 的值添在A的最后,然后删除ai,aj,这样得到一系列n-1项的新数列A1 (约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2,如此经过k次操作后得到的新数列记作Ak.设A:
的值添在A的最后,然后删除ai,aj,这样得到一系列n-1项的新数列A1 (约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2,如此经过k次操作后得到的新数列记作Ak.设A: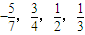 ,则A3的可能结果是( )
,则A3的可能结果是( )

