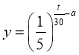题目内容
【题目】甲、乙两人玩掷骰子游戏，甲掷出的点数记为
，乙掷出的点数记为
，
若关于
的一元二次方程
有两个不相等的实数根时甲胜；方程有
两个相等的实数根时为“和”；方程没有实数根时乙胜.
（1）列出甲、乙两人“和”的各种情形；
（2）求甲胜的概率.
必要时可使用此表格
【答案】(1)详见解析;(2) 
.
【解析】试题分析:(1) 由
得
,进而求出m的可能值,列举出结果;(2)根据m,n的取值情况以及古典概型的概率公式可求得甲胜的概率.
试题解析:(1)由
得
的取值只能是
、
、
、
、
、
六种结果.其中
、
为完全平方数.
∴当且仅当
或
两种情形时， 
此时方程有两个相等的实数根，甲、乙两人“和”.
（2）
的取值只能是： 
、
、
、
、
、
六种结果.
的取值只能是： 
、
、
、
、
、
六种结果.
共有
种情形，其所有取值的符号如下表：
其中
的情形共有
种. ∴ 所求甲胜的概率
.
| 1 | 4 | 9 | 16 | 25 | 36 |
4 | — | 0 | + | + | + | + |
8 | — | — | + | + | + | + |
12 | — | — | — | + | + | + |
16 | — | — | — | 0 | + | + |
20 | — | — | — | — | + | + |
24 | — | — | — | — | + | + |
【题目】某班同学利用国庆节进行社会实践，对[25，55]岁的人群随机抽取
人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25，30) | 120 | 0.6 |
第二组 | [30，35) | 195 |
|
第三组 | [35，40) | 100 | 0.5 |
第四组 | [40，45) |
| 0.4 |
第五组 | [45，50) | 30 | 0.3 |
第六组 | [50，55] | 15 | 0.3 |
(1)补全频率分布直方图并求
的值；
(2)从年龄段在[40，50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[4，45)岁的概率.
【题目】某工厂36名工人的年龄数据如下表．
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
(2)计算(1)中样本的均值x和方差s2；
(3)36名工人中年龄在
与
之间有多少人？所占的百分比是多少(精确到0.01%)?
