题目内容
下列命题中所有正确序号为______
①在△ABC中,若sinA>sinB,则cosA<cosB;
②若b2-4c≥0,则函数y=log2(x2+bx+c)的值域为R
③如果一个数列{an}的前n项和Sn=abn+c,(a≠0,b≠1,c≠1)则此数列是等比数列的充要条件是a+c=0
④设命题p:1-
<0,命题q:-x 2+(2a+1)x-a(a+1)>0,若¬p是¬q的必要不充分条件,求实数a的取值范围0≤a≤
.
①在△ABC中,若sinA>sinB,则cosA<cosB;
②若b2-4c≥0,则函数y=log2(x2+bx+c)的值域为R
③如果一个数列{an}的前n项和Sn=abn+c,(a≠0,b≠1,c≠1)则此数列是等比数列的充要条件是a+c=0
④设命题p:1-
| 1 |
| 2x-1 |
| 1 |
| 2 |
对于①:在△ABC中,若sinA>sinB,则A>B,
由余弦函数在(0,π)是减函数,故有cosA<cosB,故①正确;
对于②:若b2-4c≥0,则x2+bx+c能取得所有正数,
∴函数y=log2(x2+bx+c)的值域为R,故②正确;
对于③:数列{an}的前n项和Sn=abn+c
可得当n≥2时,an=Sn-Sn-1=abn-1(b-1)
当n=1时,a1=S1=ab+c
接下来讨论充分性与必要性
若a+c=0,则ab+c=a(b-1)=ab1-1(b-1),
可得数列的通项为an=a(b-1)bn-1,
∵a≠0,b≠0,b≠1
∴数列{an}构成以a(b-1)为首项,公比为b的等比数列.故充分性成立;
反之,若此数列是等比数列,得
∵当n≥2时,an=abn-1(b-1),公比为b
∴a2=ab1(b-1)=ba1=b(ab+c)
∴-ab=bc?b(a+c)=0
∵b≠0,
∴a+c=0,故必要性成立,故③正确;
④∵命题p:1-
<0,
∴¬P:
≥0,即x≥1,或x<
;
∵命题q:-x 2+(2a+1)x-a(a+1)>0,
∴¬q:(x-a)[x-(a+1)]≥0,即x≥a+1,或x<a.
∵¬p是¬q的必要不充分条件,
∴
,解得实数a的取值范围0≤a≤
.
故④正确.
故答案为:①②③④.
由余弦函数在(0,π)是减函数,故有cosA<cosB,故①正确;
对于②:若b2-4c≥0,则x2+bx+c能取得所有正数,
∴函数y=log2(x2+bx+c)的值域为R,故②正确;
对于③:数列{an}的前n项和Sn=abn+c
可得当n≥2时,an=Sn-Sn-1=abn-1(b-1)
当n=1时,a1=S1=ab+c
接下来讨论充分性与必要性
若a+c=0,则ab+c=a(b-1)=ab1-1(b-1),
可得数列的通项为an=a(b-1)bn-1,
∵a≠0,b≠0,b≠1
∴数列{an}构成以a(b-1)为首项,公比为b的等比数列.故充分性成立;
反之,若此数列是等比数列,得
∵当n≥2时,an=abn-1(b-1),公比为b
∴a2=ab1(b-1)=ba1=b(ab+c)
∴-ab=bc?b(a+c)=0
∵b≠0,
∴a+c=0,故必要性成立,故③正确;
④∵命题p:1-
| 1 |
| 2x-1 |
∴¬P:
| 2x-2 |
| 2x-1 |
| 1 |
| 2 |
∵命题q:-x 2+(2a+1)x-a(a+1)>0,
∴¬q:(x-a)[x-(a+1)]≥0,即x≥a+1,或x<a.
∵¬p是¬q的必要不充分条件,
∴
|
| 1 |
| 2 |
故④正确.
故答案为:①②③④.

练习册系列答案
相关题目
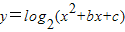 的值域为R
的值域为R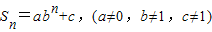 则此数列是等比数列的充要条件是a+c=0
则此数列是等比数列的充要条件是a+c=0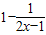 <0,命题q:-x 2+(2a+1)x-a(a+1)>0,若¬p是¬q的必要不充分条件,求实数a的取值范围0≤a≤
<0,命题q:-x 2+(2a+1)x-a(a+1)>0,若¬p是¬q的必要不充分条件,求实数a的取值范围0≤a≤ .
.