题目内容
一台机器可以按各种不同的速度运转,其生产的物件有一些会有问题,每小时生产有问题物件的多寡,随机器运转的速度而变化,下面表格中的数据是几次试验的结果.
(1)求出机器速度影响每小时生产有问题物件数的回归直线方程;
(2)若实际生产中所允许的每小时最大问题物件数为10,那么机器的速度不得超过多少转/秒?
| 速度(转/秒) | 每小时生产有问题物件数 |
| 8 | 5 |
| 12 | 8 |
| 14 | 9 |
| 16 | 11 |
(2)若实际生产中所允许的每小时最大问题物件数为10,那么机器的速度不得超过多少转/秒?
(1) y=0.7286x-0.8575;(2) 不能超过14.9019转/秒
(1)利用公式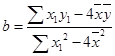 ,再根据
,再根据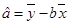 求出
求出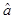 ,从而确定回归直线方程.
,从而确定回归直线方程.
(2)根据题目条件解不等式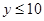 即可求出x的范围.
即可求出x的范围.
解:(1)用x表示机器速度,y表示每小时生产有问题物件数,那么4个样本数据为:(8,5)、(12,8)、(14,9)、(16,11),则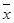 =12.5,
=12.5,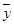 =8.25.于是回归直线的斜率为
=8.25.于是回归直线的斜率为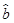 =
=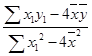 =
=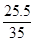 ≈0.7286,
≈0.7286,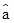 =
=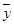 -
-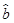
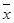 =-0.8575,所以所求的回归直线方程为y=0.7286x-0.8575.
=-0.8575,所以所求的回归直线方程为y=0.7286x-0.8575.
(2)根据公式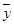 =0.7286x-0.8575,要使y≤10,则就需要0.7286x-0.8575≤10,x≤14.9019,即机器的旋转速度不能超过14.9019转/秒.
=0.7286x-0.8575,要使y≤10,则就需要0.7286x-0.8575≤10,x≤14.9019,即机器的旋转速度不能超过14.9019转/秒.
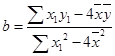 ,再根据
,再根据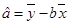 求出
求出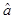 ,从而确定回归直线方程.
,从而确定回归直线方程.(2)根据题目条件解不等式
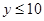 即可求出x的范围.
即可求出x的范围.解:(1)用x表示机器速度,y表示每小时生产有问题物件数,那么4个样本数据为:(8,5)、(12,8)、(14,9)、(16,11),则
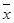 =12.5,
=12.5,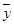 =8.25.于是回归直线的斜率为
=8.25.于是回归直线的斜率为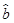 =
=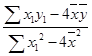 =
=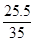 ≈0.7286,
≈0.7286,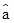 =
=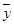 -
-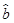
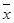 =-0.8575,所以所求的回归直线方程为y=0.7286x-0.8575.
=-0.8575,所以所求的回归直线方程为y=0.7286x-0.8575.(2)根据公式
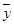 =0.7286x-0.8575,要使y≤10,则就需要0.7286x-0.8575≤10,x≤14.9019,即机器的旋转速度不能超过14.9019转/秒.
=0.7286x-0.8575,要使y≤10,则就需要0.7286x-0.8575≤10,x≤14.9019,即机器的旋转速度不能超过14.9019转/秒.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
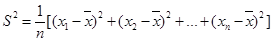 考虑,你认为哪位学生更稳定?请说明理由。
考虑,你认为哪位学生更稳定?请说明理由。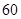 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段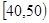 ,
,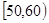 …
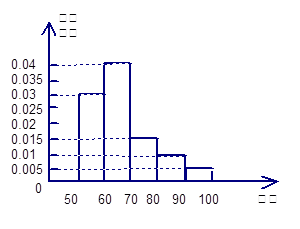
…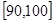 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: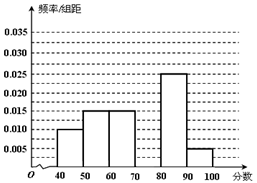
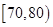 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;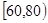 的学生中抽取一个容量为
的学生中抽取一个容量为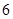 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取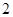 人,求至多有
人,求至多有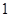 人在分数段
人在分数段 的概率.
的概率.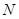 名师生志愿者,现将所有志愿者按年龄情况分为
名师生志愿者,现将所有志愿者按年龄情况分为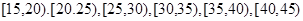 等六组,其频率分布直方图如下图所示: 已知
等六组,其频率分布直方图如下图所示: 已知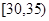 之间的志愿者共
之间的志愿者共 人.
人.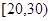 之间的志愿者人数
之间的志愿者人数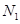 ;
;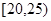 和
和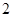 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取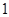 名数学教师的概率?
名数学教师的概率?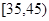 之间的志愿者(其中共有
之间的志愿者(其中共有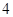 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取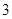 名担任后勤保障工作,其中女教师的人数为
名担任后勤保障工作,其中女教师的人数为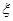 ,求
,求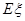 .
.
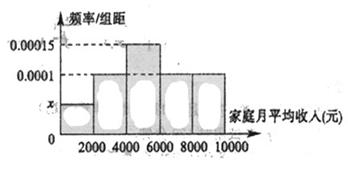
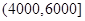 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在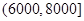 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在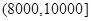 (元)间的同学不发助学金.
(元)间的同学不发助学金.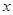 值;
值;