题目内容
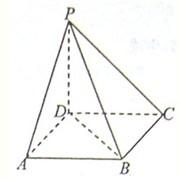 如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD.
如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD.(1)若PD=2,①求异面直线PC与BD所成的角,②求二面角D-PB-C的余弦值;
③在PB上是否存在E点,使PC⊥平面ADE,若存在,确定点E位置,若不存在说明理由;
(2)若PD=m,记二面角D-PB-C的大小为θ,若θ<60°,求m的取值范围.
分析:(1)①先建立空间直角坐标系,找到各定点的坐标,求出
与
的坐标,用向量的夹角公式求出向量
与
的夹角,利用图象判断,向量
与
的夹角就是异面直线PC与BD所成的角.
②先求出平面DPB与平面CPB的法向量,用向量夹角公式计算两个法向量的夹角,结合图象可判断,二面角的大小是两个法向量的夹角的补角,可得二面角的余弦.
③先假设在PB上存在E点,使PC⊥平 面ADE,用含参数的式子表示
,
,因为PC⊥平 面ADE,所以
•
=0,就可求参数的值,若能求出,则假设正确,否则,假设不成立.
(2)先求出平面PBD 的法向量,以及平面PBC的法向量,则两个法向量的夹角余弦的绝对值即为二面角D-PB-C余弦cosθ,
因为θ<60°,就可得到关于m的不等式,解出m的范围.
| PC |
| DB |
| PC |
| DB |
| PC |
| DB |
②先求出平面DPB与平面CPB的法向量,用向量夹角公式计算两个法向量的夹角,结合图象可判断,二面角的大小是两个法向量的夹角的补角,可得二面角的余弦.
③先假设在PB上存在E点,使PC⊥平 面ADE,用含参数的式子表示
| PE |
| AE |
| PC |
| AE |
(2)先求出平面PBD 的法向量,以及平面PBC的法向量,则两个法向量的夹角余弦的绝对值即为二面角D-PB-C余弦cosθ,
因为θ<60°,就可得到关于m的不等式,解出m的范围.
解答:解:(1)如图建立空间直角坐标系,则D(0,0,0),
A(2,0,0),C(0,2,0),P(0,0,2),B(2,2,0)
①∵
=(0,2,-2),
=(2,2,0)
∴c0s<
,
>=
=
=
∴<
,
>=60°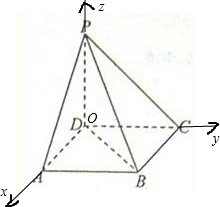
∴异面直线PC与BD所成的角为60°
②由①知
=(0,0,2),
=(2,2,0),
=(2,0,0),
=(0,2,-2)
设平面DPB的法向量
=(x1,y1,z1),平面CPB的法向量
=(x2,y2,z2)
∵
⊥
,
⊥
,
⊥
,
⊥
∴
•
=0,
•
=0,
•
=0,
•
=0
即
=0,
=0
∴取
=(1,-1,0),
=(0,1,1)
∴cos<
,
>=
=-
又∵二面角D-PB-C为锐角,∴二面角D-PB-C的余弦值为
.
③假设在PB上存在E点,使PC⊥平 面ADE,记
=λ
∵
=(2,2,-2),∴
=(2λ,2λ,-2λ),∴E(2λ,2λ,2-2λ)
∴
=(2λ-2,2λ,2-2λ),若PC⊥平面ADE,则有PC⊥AE,
即
•
=8λ-4=0∴λ=
,E(1,1,1)
又∵AD⊥面PDC,∴PC⊥AD,∴PC⊥平面ADE.
∴存在E点且E为PB的中点时,PC⊥平面ADE.
(2)依题意P(0,0,m)
∵PD⊥AC,BD⊥AC,∴AC⊥平面PBD
∴
=(-2,2,0)为平面PBD的一个法向量
=(-2,0,0),
=(0,2,-m)
设平面PBC的法向量为
=(a,b,c)
则
•
=0,
•
=0
∴
,取
=(0,m,2)
∵|cosθ|=|cos<
,
>|=|
|=
∵θ<60°,∴|cosθ|=cosθ>
∴
>
,解得m>2
∴m的取值范围为(2,+∞)
A(2,0,0),C(0,2,0),P(0,0,2),B(2,2,0)
①∵
| PC |
| DB |
∴c0s<
| PC |
| DB |
| ||||
|
|
| 4 | ||||
2
|
| 1 |
| 2 |
∴<
| PC |
| DB |

∴异面直线PC与BD所成的角为60°
②由①知
| DP |
| DB |
| CB |
| PC |
设平面DPB的法向量
| m |
| n |
∵
| DP |
| m |
| DB |
| m |
| CB |
| n |
| PC |
| n |
∴
| DP |
| m |
| DB |
| m |
| CB |
| n |
| PC |
| n |
即
|
|
∴取
| m |
| n |
∴cos<
| m |
| n |
| -1 | ||||
|
| 1 |
| 2 |
又∵二面角D-PB-C为锐角,∴二面角D-PB-C的余弦值为
| 1 |
| 2 |
③假设在PB上存在E点,使PC⊥平 面ADE,记
| PE |
| PB |
∵
| PB |
| PE |
∴
| AE |
即
| PC |
| AE |
| 1 |
| 2 |
又∵AD⊥面PDC,∴PC⊥AD,∴PC⊥平面ADE.
∴存在E点且E为PB的中点时,PC⊥平面ADE.
(2)依题意P(0,0,m)
∵PD⊥AC,BD⊥AC,∴AC⊥平面PBD
∴
| AC |
| BC |
| PC |
设平面PBC的法向量为
| t |
则
| t |
| BC |
| t |
| PC |
∴
|
| t |
∵|cosθ|=|cos<
| AC |
| T |
| ||||
|
|
| m | ||||
|
∵θ<60°,∴|cosθ|=cosθ>
| 1 |
| 2 |
∴
| m | ||||
|
| 1 |
| 2 |
∴m的取值范围为(2,+∞)
点评:本题主要考查在空间几何体中,异面直线所成角,二面角的求法,以及线面垂直的证明,综合考察了学生的识图能力,空间想象力,转化能力以及计算能力.

练习册系列答案
相关题目
 如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求:
如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求: 如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°,
如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°, (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB= 如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC=
如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC= 及点D的坐标.
及点D的坐标.