题目内容
已知数列{ }的前n项和
}的前n项和 ,数列{
,数列{ }满足
}满足 =
= .
.
(I)求证:数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求满足
,求满足 的
的 的最大值.
的最大值.
 }的前n项和
}的前n项和 ,数列{
,数列{ }满足
}满足 =
= .
.(I)求证:数列{
 }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;(Ⅱ)设
 ,数列
,数列 的前
的前 项和为
项和为 ,求满足
,求满足 的
的 的最大值.
的最大值.(I)  (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
试题分析:(Ⅰ)在
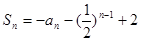 中,令n=1,可得
中,令n=1,可得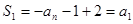 ,即
,即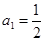 .
. 当
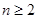 时,
时,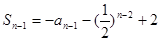 ∴
∴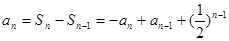 ,
,∴
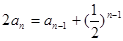 ,即
,即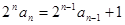 .∵
.∵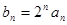 ,∴
,∴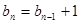 ,即当
,即当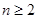 时,
时,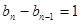 . ……又
. ……又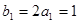 ,∴数列{bn}是首项和公差均为1的等差数列.
,∴数列{bn}是首项和公差均为1的等差数列.于是
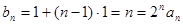 ,∴
,∴ .
. (Ⅱ)∵
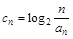
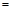
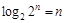 ,
,∴
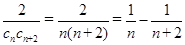 ,
, ∴
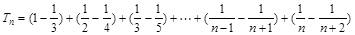 =
=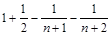 .
.由
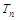
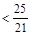 ,得
,得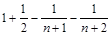
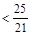 ,即
,即 ,
,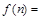
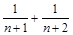 单调递减,∵
单调递减,∵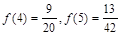 ,
,∴
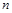 的最大值为4.
的最大值为4.点评:本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力.

练习册系列答案
相关题目
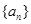 是公比为q的等比数列.
是公比为q的等比数列. 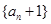 不是等比数列.
不是等比数列.  的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 使得
使得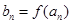 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称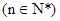 .
.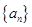 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若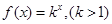 是数列
是数列 的首项为2010,
的首项为2010,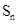 是数列
是数列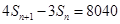 ,证明
,证明 ,
, ,和数列1,
,和数列1,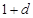 ,
,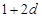 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.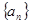 的通项为
的通项为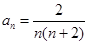 ,则其前
,则其前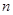 项和
项和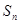 为( )
为( )
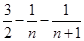
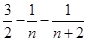
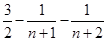
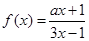 ,且方程
,且方程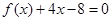 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的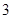 倍,记等差数列
倍,记等差数列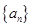 、
、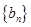 的前
的前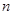 项和分别为
项和分别为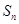 ,
,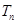 且
且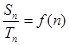 (
(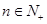 )。
)。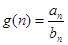 ,求
,求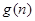 的最大值;
的最大值;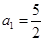 ,数列
,数列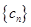 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.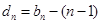 ,
,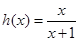 .
. .
.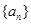 中,
中,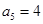 ,前9项和
,前9项和 ( )
( )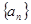 中,已知
中,已知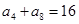 ,则
,则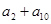 为 ( )
为 ( )
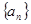 是等差数列,且
是等差数列,且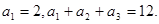
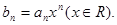 求数列
求数列 前n项和的公式.
前n项和的公式.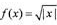 ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )