题目内容
已知定义在区间 上的函数
上的函数 的图像关于直线
的图像关于直线 对称,当
对称,当 时,
时, ,如果关于
,如果关于 的方程
的方程 有解,记所有解的和为S, 则S不可能为
有解,记所有解的和为S, 则S不可能为
A B
B  C
C  D
D 
 上的函数
上的函数 的图像关于直线
的图像关于直线 对称,当
对称,当 时,
时, ,如果关于
,如果关于 的方程
的方程 有解,记所有解的和为S, 则S不可能为
有解,记所有解的和为S, 则S不可能为A
 B
B  C
C  D
D 
A
(Ⅲ)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案
解答:解:作函数f(x)的图象(如图),

显然,若f(x)=a有解,则a∈[-1,0]
①-1<a<- ,f(x)=a有4解,S=-π②
,f(x)=a有4解,S=-π②
a=- ,f(x)=a有三解,S=-
,f(x)=a有三解,S=- π
π
③- <a<0或a=-1,f(x)=a有2解,S=
<a<0或a=-1,f(x)=a有2解,S=
故选A.
解答:解:作函数f(x)的图象(如图),

显然,若f(x)=a有解,则a∈[-1,0]
①-1<a<-
 ,f(x)=a有4解,S=-π②
,f(x)=a有4解,S=-π②a=-
 ,f(x)=a有三解,S=-
,f(x)=a有三解,S=- π
π③-
 <a<0或a=-1,f(x)=a有2解,S=
<a<0或a=-1,f(x)=a有2解,S=
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 + 1 ,则f ( 0) = ( )
+ 1 ,则f ( 0) = ( )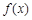 满足:①定义域为
满足:①定义域为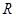 ;②
;②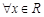 ,有
,有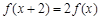 ;③当
;③当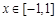 时,
时,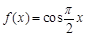 ,则方程
,则方程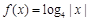 在区间
在区间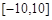 内的解个数是
内的解个数是 



 的方程
的方程 有一个负根,但没有正根,则实数
有一个负根,但没有正根,则实数 的取值范围是
的取值范围是  ,
, 的奇偶性;
的奇偶性; 上是减函数。
上是减函数。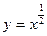 ,②
,②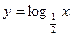 ,③
,③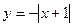 ,④
,④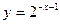 ,其中在区间[0,+
,其中在区间[0,+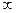 )上单调递
)上单调递 在区间
在区间 上无零点,则函数
上无零点,则函数 的递减区间是
的递减区间是




 的零点个数为 ( )
的零点个数为 ( ) 在
在 为增函数,那么实数
为增函数,那么实数 的取值范围是( )
的取值范围是( )


