题目内容
12.若函数f(x)是幂函数,且满足$\frac{f(4)}{f(2)}$=3,则f($\frac{1}{2}$)的值为( )| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
分析 设f(x)=xα(α为常数),由满足$\frac{f(4)}{f(2)}$=3,可得α=log23.$f(x)={x}^{lo{g}_{2}3}$.代入即可得出.
解答 解:设f(x)=xα(α为常数),
∵满足$\frac{f(4)}{f(2)}$=3,∴$\frac{{4}^{α}}{{2}^{α}}$=3,∴α=log23.
∴$f(x)={x}^{lo{g}_{2}3}$.
则f($\frac{1}{2}$)=${2}^{-lo{g}_{2}3}$=$\frac{1}{3}$.
故选:D.
点评 本题考查了指数函数与对数函数的运算法则、幂函数的定义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.下列4个命题是真命题的是( )
①“若x2+y2=0,则x、y均为零”的逆命题
②“相似三角形的面积相等”的否命题
③“若A∩B=A,则A⊆B”的逆否命题
④“末位数字不是零的数可被3整除”的逆否命题.
①“若x2+y2=0,则x、y均为零”的逆命题
②“相似三角形的面积相等”的否命题
③“若A∩B=A,则A⊆B”的逆否命题
④“末位数字不是零的数可被3整除”的逆否命题.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
7.下列函数中能用二分法求零点的是( )
| A. | 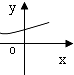 | B. |  | C. | 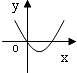 | D. | 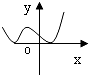 |
 执行程序框图,若输入的a,b,k分别为1,2,3,则输出的M=$\frac{15}{8}$.
执行程序框图,若输入的a,b,k分别为1,2,3,则输出的M=$\frac{15}{8}$.