题目内容
17.在直角坐标系中,已知M(2,1)和直线L:x-y=0,试在直线L上找一点P,在X轴上找一点Q,使三角形MPQ的周长最小,最小值为$\sqrt{10}$.分析 作出M(2,1)关于直线L:x-y=0的对称点N(1,2),作出M(2,1)关于x轴的对称点E(2,-1),连结MN,交直线L于P,交x轴于E,从而得到三角形MPQ的周长最小时,最小值为|NE|.
解答 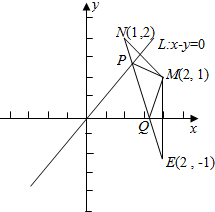 解:如图,作出M(2,1)关于直线L:x-y=0的对称点N(1,2),
解:如图,作出M(2,1)关于直线L:x-y=0的对称点N(1,2),
作出M(2,1)关于x轴的对称点E(2,-1),
连结MN,交直线L于P,交x轴于E,
∵MP=PN,MQ=QE,∴三角形MPQ的周长为线段NE的长,
由两点间线段最短得此时三角形MPQ的周长最小,
∴三角形MPQ的周长最小时,最小值为:
|NE|=$\sqrt{(1-2)^{2}+(2+1)^{2}}$=$\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题考查三角形周长的最小值的求法,是中档题,解题时要认真审题,注意转化思想的合理运用.

练习册系列答案
相关题目
8.函数f(x)=(a+1)tan2x+3sinx+a2-3a-4为奇函数的充要条件是( )
| A. | a=4 | B. | a=-1 | C. | a=4或a=-1 | D. | a∈R |
5.已知集合A=B={(x,y)|x,y∈R},映射f:A→B,(x,y)→(x+y,x-y),则在映射f下,象(2,1)的原象是( )
| A. | ($\frac{3}{2}$,-$\frac{1}{2}$) | B. | ($\frac{3}{2}$,$\frac{1}{2}$) | C. | (3,1) | D. | (1,3) |
12.若函数f(x)是幂函数,且满足$\frac{f(4)}{f(2)}$=3,则f($\frac{1}{2}$)的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
2.函数f(x)=$sin({2x+\frac{π}{6}})$的最小正周期和振幅分别是( )
| A. | π,1 | B. | π,2 | C. | 2π,1 | D. | 2π,2 |
9.函数f(x)=$\sqrt{1-(\frac{1}{2})^{x}}+\frac{1}{3-x}$的定义域为( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (0,3)∪(3,+∞) | D. | [0,3)∪(3,+∞) |
6.下列各点中,与点(1,2)位于直线x+y-1=0的同一侧的是( )
| A. | (0,0) | B. | (-1,1) | C. | (-1,3) | D. | (2,-3) |