题目内容
已知函数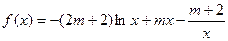
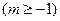 .
.
(Ⅰ)讨论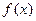 的单调性;
的单调性;
(Ⅱ)设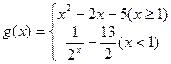 .当
.当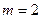 时,若对任意
时,若对任意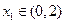 ,
,
存在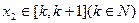 ,使
,使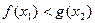 ,求实数
,求实数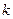 的最小值
的最小值
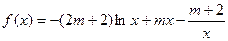
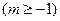 .
.(Ⅰ)讨论
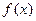 的单调性;
的单调性;(Ⅱ)设
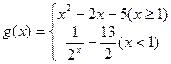 .当
.当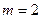 时,若对任意
时,若对任意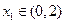 ,
,存在
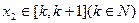 ,使
,使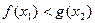 ,求实数
,求实数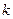 的最小值
的最小值(Ⅰ) 当
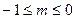 时,函数
时,函数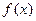 的单调递增区间为
的单调递增区间为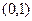 ,单调递减区间为
,单调递减区间为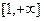 ;
;当
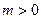 时,函数
时,函数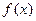 单调递增区间为
单调递增区间为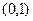 和
和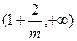 ,单调递减区间
,单调递减区间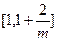
(Ⅱ)4
解:(Ⅰ)由题,函数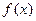 的定义域为
的定义域为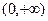
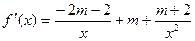
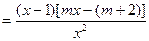
(1)若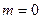 ,则
,则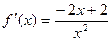 ,
,
从 而当
而当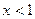 时,
时,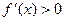 ;当
;当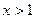 时,
时,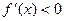 ,
,
此时函数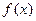 的单调递增区间为
的单调递增区间为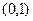 ,单
,单 调递减区间为
调递减区间为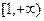 ;------------3分
;------------3分
(2)若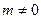 ,则
,则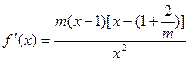 ,
,
①当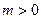 时,因为
时,因为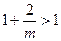 ,从而当
,从而当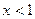 或
或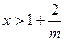 时,
时,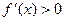 ;当
;当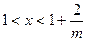 时,
时,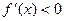 ,
,
此时函数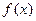 的单调递增区间为
的单调递增区间为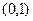 和
和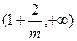 ,单调递减区间为
,单调递减区间为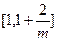 ;
;
②当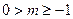 时,
时,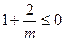 ,
,
函数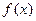 的单调递增区间为
的单调递增区间为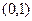 ,单调递减区间为
,单调递减区间为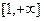 ;
;
综上所述,当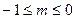 时,函数
时,函数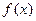 的单调递增区间为
的单调递增区间为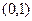 ,单调递减区间为
,单调递减区间为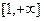 ;
;
当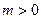 时,函数
时,函数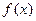 单调递增区间为
单调递增区间为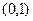 和
和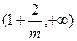 ,单调递减区间
,单调递减区间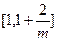 8分
8分
(Ⅱ)由(Ⅰ)可得当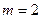 时,函数
时,函数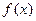 在区间
在区间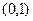 上单调递增,在
上单调递增,在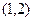 上单调递减,
上单调递减,
所以在区间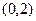 上,
上,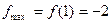 ,
,
由题,对任意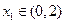 ,存在
,存在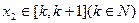 ,使
,使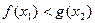 ,
,
从而存在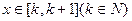 ,使
,使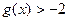 ,
,
即只需函数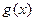 在区间
在区间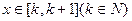 上的最小值大于
上的最小值大于 ,
,
又当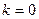 时,
时, 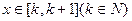 时,
时,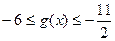 ,不符
,不符
所以在区间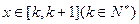 上
上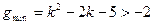 ,解得
,解得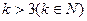 ,
,
所以实数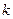 的最小值为4. -------------15分
的最小值为4. -------------15分
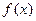 的定义域为
的定义域为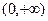
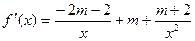
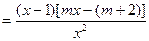
(1)若
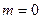 ,则
,则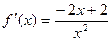 ,
,从
 而当
而当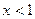 时,
时,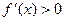 ;当
;当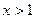 时,
时,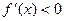 ,
,此时函数
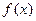 的单调递增区间为
的单调递增区间为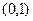 ,单
,单 调递减区间为
调递减区间为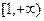 ;------------3分
;------------3分(2)若
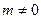 ,则
,则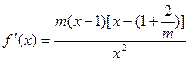 ,
,①当
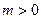 时,因为
时,因为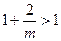 ,从而当
,从而当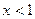 或
或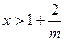 时,
时,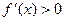 ;当
;当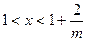 时,
时,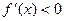 ,
,此时函数
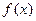 的单调递增区间为
的单调递增区间为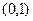 和
和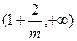 ,单调递减区间为
,单调递减区间为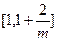 ;
;②当
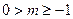 时,
时,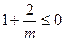 ,
,函数
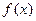 的单调递增区间为
的单调递增区间为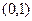 ,单调递减区间为
,单调递减区间为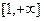 ;
;综上所述,当
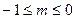 时,函数
时,函数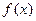 的单调递增区间为
的单调递增区间为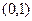 ,单调递减区间为
,单调递减区间为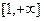 ;
;当
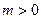 时,函数
时,函数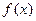 单调递增区间为
单调递增区间为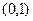 和
和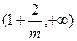 ,单调递减区间
,单调递减区间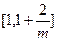 8分
8分(Ⅱ)由(Ⅰ)可得当
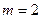 时,函数
时,函数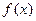 在区间
在区间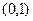 上单调递增,在
上单调递增,在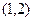 上单调递减,
上单调递减,所以在区间
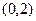 上,
上,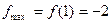 ,
,由题,对任意
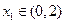 ,存在
,存在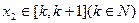 ,使
,使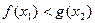 ,
,从而存在
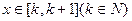 ,使
,使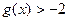 ,
,即只需函数
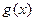 在区间
在区间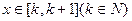 上的最小值大于
上的最小值大于 ,
,又当
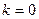 时,
时, 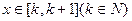 时,
时,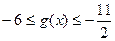 ,不符
,不符所以在区间
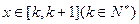 上
上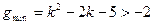 ,解得
,解得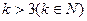 ,
,所以实数
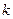 的最小值为4. -------------15分
的最小值为4. -------------15分
练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
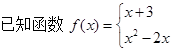

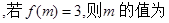 ( )
( )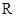 上的函数
上的函数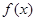 满足
满足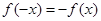 ,当
,当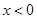 时,
时,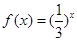 ,则
,则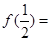
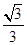
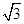
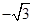
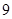
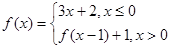 ,则
,则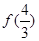 的值为( )
的值为( )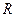 的函数
的函数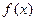 是偶函数,当
是偶函数,当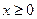 时,
时,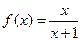 .
.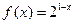 在区间
在区间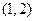 上有解
上有解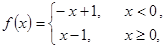 则不等式
则不等式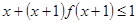 的解集是
的解集是 



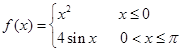 则集合
则集合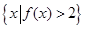 等于 ( )
等于 ( )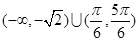



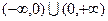 上的奇函数
上的奇函数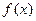 ,在
,在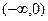 单调递增,且
单调递增,且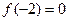 ,则不等式
,则不等式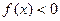 的解集是_________________
的解集是_________________ 给出函数f (x)=2-x-x2,若对于任意x∈[0,+∞),恒有fK(x)=f(x),则( )
给出函数f (x)=2-x-x2,若对于任意x∈[0,+∞),恒有fK(x)=f(x),则( )