题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知向量m=(cos A,cos B),n=(2c+b,a),且m⊥n.
(I)求角A的大小;
(Ⅱ)若a=4,求△ABC面积的最大值.
【答案】
(Ⅰ)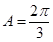 (Ⅱ)
(Ⅱ)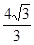 .
.
【解析】本试题主要是考查了解三角形的运用。利用正弦定理和余弦定理表示角和变的关系式,并结合三角形的面积公式得到结论。
(1)利用向量的数量积,表示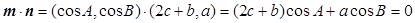 ,然后正弦定理可得
,然后正弦定理可得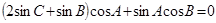 ,化简得到角A。
,化简得到角A。
(2)由余弦定理可得,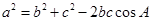 ,即
,即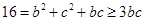 (当且仅当
(当且仅当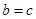 时取等号),故
时取等号),故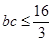 .结合均值不等式得到面积的最大值。
.结合均值不等式得到面积的最大值。
解:(Ⅰ)∵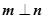 ,∴
,∴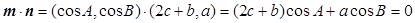 ,由正弦定理可得
,由正弦定理可得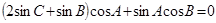 ,即
,即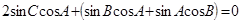 ,整理可得
,整理可得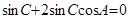 .…………(5分)
.…………(5分)
∵0<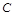 <
< ,∴
,∴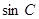 >0,∴
>0,∴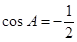 ,∴
,∴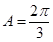 .……………………(6分)
.……………………(6分)
(Ⅱ)由余弦定理可得,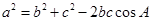 ,即
,即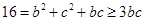 (当且仅当
(当且仅当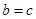 时取等号),故
时取等号),故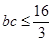 . ………(9分)
. ………(9分)
故△ABC的面积为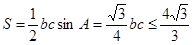 ,当且仅当
,当且仅当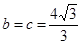 时,△ABC的面积取得最大值
时,△ABC的面积取得最大值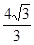

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |