题目内容
 已知双曲线C:
已知双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| AF |
| FB |
A、
| ||
B、
| ||
C、
| ||
D、
|
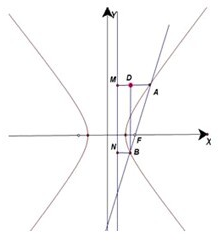
分析:设双曲线的有准线为l,过A、B分别作AM⊥l于M,BN⊥l于N,BD⊥AM于D,由直线AB的斜率可知直线AB的倾斜角,进而推|AD|=
|AB|,由双曲线的第二定义|AM|-|BN|=|AD|,进而根据
=4
,求得离心率.
| 1 |
| 2 |
. |
| AF |
. |
| FB |
解答:解:设双曲线C:
-
=1的右准线为l,
过A、B分别作AM⊥l于M,BN⊥l于N,BD⊥AM于D,
由直线AB的斜率为
,
知直线AB的倾斜角为60°
∴∠BAD=60°
|AD|=
|AB|,
由双曲线的第二定义有:
|AM|-|BN|=|AD|=
(|
|-|
|)
=
|AB|=
(|
|+|
|)
∴
•3|
|=
|
|,∴e=
故选A.
| x2 |
| a2 |
| y2 |
| b2 |
过A、B分别作AM⊥l于M,BN⊥l于N,BD⊥AM于D,
由直线AB的斜率为
| 3 |
知直线AB的倾斜角为60°
∴∠BAD=60°
|AD|=
| 1 |
| 2 |
由双曲线的第二定义有:
|AM|-|BN|=|AD|=
| 1 |
| e |
| AF |
| FB |
=
| 1 |
| 2 |
| 1 |
| 2 |
| AF |
| FB |
∴
| 1 |
| e |
| FB |
| 5 |
| 2 |
| FB |
| 6 |
| 5 |
故选A.
点评:本题主要考查了双曲线的定义.解题的关键是利用了双曲线的第二定义,找到了已知条件与离心率之间的联系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目