题目内容
【题目】如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′,连接EF,A′B. 
(1)求证:A′D⊥EF;
(2)求二面角A′﹣EF﹣D的余弦值.
【答案】
(1)证明:在正方形ABCD中,有AD⊥AE,CD⊥CF
则A'D⊥A'E,A'D⊥A'F
又A'E∩A'F=A'
∴A'D⊥平面A'EF
而EF平面A'EF,∴A'D⊥EF
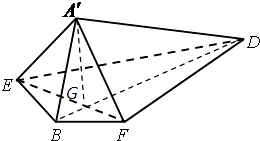
(2)方法一:连接BD交EF于点G,连接A'G
∵在正方形ABCD中,点E是AB的中点,点F是BC的中点,
∴BE=BF,DE=DF,
∴点G为EF的中点,
且BD⊥EF
∵正方形ABCD的边长为2,∴A'E=A'F=1,∴A'G⊥EF
∴∠A'GD为二面角A'﹣EF﹣D的平面角
由(1)可得A'D⊥A'G,
∴△A'DG为直角三角形
∵正方形ABCD的边长为2,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
又A'D=2
∴ ![]()
∴ 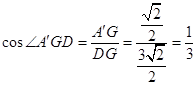
∴二面角A'﹣EF﹣D的余弦值为 ![]()
方法二:∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,
∴BE=BF=A'E=A'F=1,
∴ ![]()
∴A'E2+A'F2=EF2,∴A'E⊥A'F
由(1)得A'D⊥平面A'EF,
∴分别以A'E,A'F,A'D为x,y,z轴建立如图所示的空间直角
坐标系A'﹣xyz,
则A'(0,0,0),E(1,0,0),F(0,1,0),D(0,0,2)
∴ ![]() ,
, ![]() ,
,
设平面DEF的一个法向量为 ![]() ,则由
,则由  ,
,
可取 ![]()
又平面A'EF的一个法向量可取 ![]()
∴ 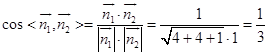
∴二面角A'﹣EF﹣D的余弦值为 ![]() .
.
【解析】(1)根据平面图形折叠后的不变量可得A'D⊥A'E,A'D⊥A'F,然后利用线面垂直的判定得到线面垂直,从而得到线线垂直;(2)由题意可得BE=BF,DE=DF,连结BD交EF于点G,连接A'G,则可证明∠A'GD为二面角A'﹣EF﹣D的平面角,然后利用解直角三角形即可得到答案.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.

【题目】某市为了普及法律知识,增强市民的法制观念,针对本市特定人群举办网上学法普法考试.为了解参考人群的法律知识水平,从一次普法考试中随机抽取了50份答卷进行分析,得到这50份答卷成绩的统计数据如下:
成绩分组 |
|
|
|
|
|
|
频数 | 2 | 5 | 12 | 16 | 10 | 5 |
(1)在答题卡的图中作出样本数据的频率分布直方图;
(2)试根据统计数据,估计本次普法考试的平均成绩![]() 和中位数( 同一组中的数据用该组区间的中点值作代表);
和中位数( 同一组中的数据用该组区间的中点值作代表);
(3)已知该市有100 万人参加考试,得分低于60 分的需要重考(不低于60 分为合格,不再重考).若每次重考的合格率都比上一次考试低6 个百分点,试估计第3 次重考的人数.