题目内容
已知函数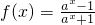 (a>0且a≠1),设函数
(a>0且a≠1),设函数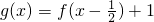 .
.
(1)求证:f(x)是奇函数;
(2)求g(x)+g(1-x)及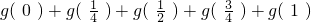 的值;
的值;
(3)是否存在正整数a,使不等式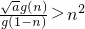 对一切n∈N*都成立,若存在,求出正整数a的最小值;不存在,说明理由;
对一切n∈N*都成立,若存在,求出正整数a的最小值;不存在,说明理由;
(4)结合本题加以推广:设F(x)是R上的奇函数,请你写出一个函数G(x)的解析式;并根据第(2)小题的结论,猜测函数G(x)满足的一般性结论.
解:(1)任取x∈R,于是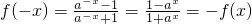 ,所以f(x)是奇函数. …
,所以f(x)是奇函数. …
(2)由(1)知f(0)=0,所以 ,…
,…
 .…
.…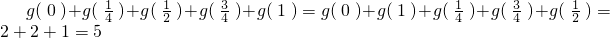 .
.
(3)假设存在正整数a,使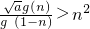 对一切n∈N*都成立.
对一切n∈N*都成立.
由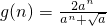 ,
,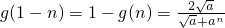 ,得
,得 .…
.…
当a=1和a=2时,不等式an>n2显然不成立.…
猜想当a≥3时,an≥3n>n2.…
下面证明3n>n2对一切n∈N*都成立:
①当n=1时,显然3>1.
②当n≥2时,3n=(1+2)n=1+2Cn1+4Cn2+…+Cnn×2n≥1+2n+2n(n-1)=2n2+1>n2成立.
则3n>n2对一切n∈N*都成立.所以存在最小正整数a=3.…
证法二:
①当n=1时,3>1,当n=2时,9>4,不等式成立.
②假设当n=k(k≥2)时,3k>k2,
则当n=k+1时,3k+1=3×3k>3k2=k2+k2+k2>k2+2k+1=(k+1)2,不等式也成立.…
则3n>n2对一切n∈N*都成立.所以存在最小正整数a=3.…
(4)如设F(x)=x3,G(x)=(x-a)3+b等均可.…
则函数G(x)满足的一般性结论为G(a)=b,G(x)+G(2a-x)=2b.…
形如设G(x)=F(x-a)+b.G(x)满足的性质为:G(a)=b,G(x)+G(2a-x)=2b.
或 则
则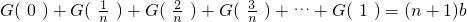 等…
等…
分析:(1)本小题中的由奇函数的定义可知,只须验证f(-x)=-f(x),由此即可得到正确答案;
(2)由(1)知f(0)=0,所以 以及g(x)+g(1-x)=2,从而求得
以及g(x)+g(1-x)=2,从而求得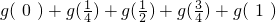 的值;
的值;
(3)对于存在性问题,可先假设存在,即假设存在正整数a,使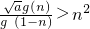 对一切n∈N*都成立,再利用二项式定理(解法一)或者数学归纳法(解法二)进行证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
对一切n∈N*都成立,再利用二项式定理(解法一)或者数学归纳法(解法二)进行证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(4)如设F(x)=x3,G(x)=(x-a)3+b等均可,则函数G(x)满足的一般性结论为G(a)=b,G(x)+G(2a-x)=2b等.
点评:本题考查函数奇偶性的性质、指数函数综合题、二项式定理或者数学归纳法等基础知识,考查运算求解能力,考查归与转化思想.属于基础题.
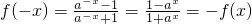 ,所以f(x)是奇函数. …
,所以f(x)是奇函数. …(2)由(1)知f(0)=0,所以
 ,…
,… .…
.…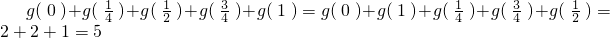 .
.(3)假设存在正整数a,使
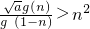 对一切n∈N*都成立.
对一切n∈N*都成立.由
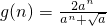 ,
,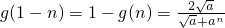 ,得
,得 .…
.…当a=1和a=2时,不等式an>n2显然不成立.…
猜想当a≥3时,an≥3n>n2.…
下面证明3n>n2对一切n∈N*都成立:
①当n=1时,显然3>1.
②当n≥2时,3n=(1+2)n=1+2Cn1+4Cn2+…+Cnn×2n≥1+2n+2n(n-1)=2n2+1>n2成立.
则3n>n2对一切n∈N*都成立.所以存在最小正整数a=3.…
证法二:
①当n=1时,3>1,当n=2时,9>4,不等式成立.
②假设当n=k(k≥2)时,3k>k2,
则当n=k+1时,3k+1=3×3k>3k2=k2+k2+k2>k2+2k+1=(k+1)2,不等式也成立.…
则3n>n2对一切n∈N*都成立.所以存在最小正整数a=3.…
(4)如设F(x)=x3,G(x)=(x-a)3+b等均可.…
则函数G(x)满足的一般性结论为G(a)=b,G(x)+G(2a-x)=2b.…
形如设G(x)=F(x-a)+b.G(x)满足的性质为:G(a)=b,G(x)+G(2a-x)=2b.
或
 则
则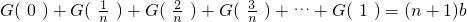 等…
等…分析:(1)本小题中的由奇函数的定义可知,只须验证f(-x)=-f(x),由此即可得到正确答案;
(2)由(1)知f(0)=0,所以
 以及g(x)+g(1-x)=2,从而求得
以及g(x)+g(1-x)=2,从而求得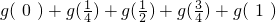 的值;
的值;(3)对于存在性问题,可先假设存在,即假设存在正整数a,使
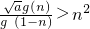 对一切n∈N*都成立,再利用二项式定理(解法一)或者数学归纳法(解法二)进行证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
对一切n∈N*都成立,再利用二项式定理(解法一)或者数学归纳法(解法二)进行证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.(4)如设F(x)=x3,G(x)=(x-a)3+b等均可,则函数G(x)满足的一般性结论为G(a)=b,G(x)+G(2a-x)=2b等.
点评:本题考查函数奇偶性的性质、指数函数综合题、二项式定理或者数学归纳法等基础知识,考查运算求解能力,考查归与转化思想.属于基础题.

练习册系列答案
相关题目
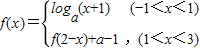 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )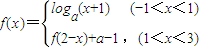 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( ) (a>0且a为常数).
(a>0且a为常数). 对x∈[-
对x∈[- ,+∞)恒成立,求a的取值范围.
,+∞)恒成立,求a的取值范围. 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数 ,(
,(