题目内容
已知等差数列an是递增数列,且满足a5=3,S6=12.(1)求数列an的通项公式;
(2)令
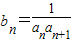 ,数列bn的前n项和Sn,若存在整数t,使Sn≤t对任意自然数n∈N*恒成立,求t的最小值.
,数列bn的前n项和Sn,若存在整数t,使Sn≤t对任意自然数n∈N*恒成立,求t的最小值.
【答案】分析:(1)由a5=3,S6=12列出关于首项和公关差的方程组,把其值代入通项公式即可.
(2)由an的通项公式得出bn的通项公式,然后进行裂项,每一项都变成差的形式,相加可抵消,最后剩余两项,易于判断Sn小于哪一个整数.
解答:解:(1)根据题意: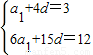 ,解得
,解得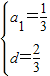 ,(3分)
,(3分)
故等差数列{an}的通项公式为an=a1+(n-1)•d=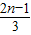 (6分)
(6分)
(2)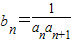 =
=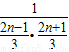 =
=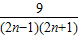 =
= (
(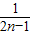 -
-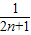 ),
),
Sn= [(1-
[(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(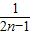 -
-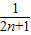 )]=
)]= [(1-
[(1-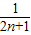 )]=
)]= (1-
(1-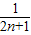 )<
)< (12分)
(12分)
∵t是整数,∴t的最小值是5.(15分)
点评:本题考查了等差数列的通项公式,数列求和的裂项法,求an有两种方法,一种是an=am+(n-m)d,另一种利用通项公式,求首项和公差;用裂项法求和时,注意项的形式,分子上是一个常数,分母上可分解成两个关于n的一次式相乘.
(2)由an的通项公式得出bn的通项公式,然后进行裂项,每一项都变成差的形式,相加可抵消,最后剩余两项,易于判断Sn小于哪一个整数.
解答:解:(1)根据题意:
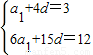 ,解得
,解得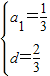 ,(3分)
,(3分)故等差数列{an}的通项公式为an=a1+(n-1)•d=
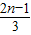 (6分)
(6分)(2)
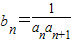 =
=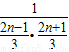 =
=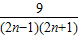 =
= (
(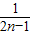 -
-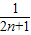 ),
),Sn=
 [(1-
[(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(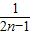 -
-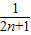 )]=
)]= [(1-
[(1-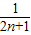 )]=
)]= (1-
(1-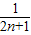 )<
)< (12分)
(12分)∵t是整数,∴t的最小值是5.(15分)
点评:本题考查了等差数列的通项公式,数列求和的裂项法,求an有两种方法,一种是an=am+(n-m)d,另一种利用通项公式,求首项和公差;用裂项法求和时,注意项的形式,分子上是一个常数,分母上可分解成两个关于n的一次式相乘.

练习册系列答案
相关题目