题目内容

【题目】已知函数f（x）= 的定义域是R，则实数m的取值范围是

【答案】[0，8]
【解析】解：∵f（x）= 的定义域为R， ∴mx2+mx+2≥0在R上恒成立，
①当m=0时，有2＞0在R上恒成立，故符合条件；
②当m≠0时，由 ，解得0＜m≤8，
综上，实数m的取值范围是[0，8]．
所以答案是：[0，8]．
【考点精析】利用函数的定义域及其求法对题目进行判断即可得到答案，需要熟知求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零．

练习册系列答案
相关题目

【题目】已知偶函数f（x）的定义域为R，且在（﹣∞，0）上是增函数，则f（﹣ ）与f（a2﹣a+1）（a∈R）的大小关系是（ ）
A.f（﹣ ）≤f（a2﹣a+1）
B.f（﹣ ）≥f（a2﹣a+1）?
C.f（﹣ ）＜f（a2﹣a+1）
D.f（﹣ ）＞f（a2﹣a+1）

【题目】某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按元/度收费，超过200度但不超过400度的部分按元/度收费，超过400度的部分按1.0元/度收费．

（Ⅰ）求某户居民用电费用（单位：元）关于月用电量（单位：度）的函数解析式；

（Ⅱ）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的占，求， 的值；

（Ⅲ）在满足（Ⅱ）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点代替，记为该居民用户1月份的用电费用，求的分布列和数学期望．

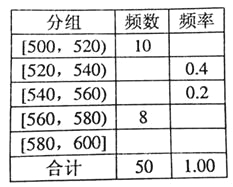
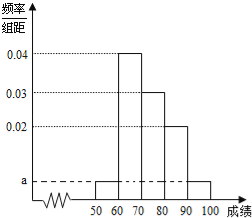
【题目】某中学为了了解全校学生的阅读情况，在全校采用随机抽样的方法抽取了60名学生（其中初中组和高中组各30名）进行问卷调查，并将他们在一个月内去图书馆的次数进行了统计，将每组学生去图书馆的次数分为5组： ，分别制作了如图所示的频率分布表和频率分布直方图.

分组

人数

频率

3

9

9

0.2

0.1

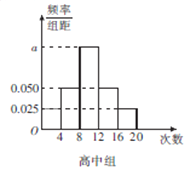
（1）完成频率分布表，并求出频率分布直方图中的值；

（2）在抽取的60名学生中，从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人，并用 表示抽得的高中组的人数，求的分布列和数学期望.

【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果，结果有50个特等品.将这50个水果的质量数据分组，得到下边的频率分布表.

（1）估计该水果的质量不少于560g的概率；

（2）若在某批水果的检测中，发现有15个特等品，据此估计该批水果中没有达到特等品的个数.

【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束，欲令‘落一形’埵（同垛）之．问底子（每层三角形边茭草束数，等价于层数）几何？”中探讨了“垛枳术”中的落一形垛（“落一形”即是指顶上1束，下一层3束，再下一层6束，…，成三角锥的堆垛，故也称三角垛，如图，表示第二层开始的每层茭草束数），则本问题中三角垛底层茭草总束数为 ．

【题目】已知函数 .

（1）若曲线在和处的切线互相平行，求的值；

（2）求函数的单调区间.

【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．

（1）求图中a的值；

（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；

（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．

【题目】“杨辉三角”又称“贾宪三角”，是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算，而杨辉在公元1261年所著的《详解九章算法》一书中，记录了贾宪三角形数表，并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数是（ ）

A. B. C. D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网