题目内容
选修4一1：几何证明选讲
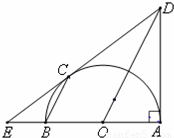
如图，C是以AB为直径的半圆O上的一点，过C的直线交直线AB于E，交过A点的切线于D，BC∥OD．
（Ⅰ）求证：DE是圆O的切线；
（Ⅱ）如果AD=AB=2，求EB．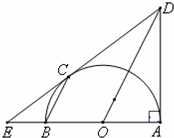
如图，C是以AB为直径的半圆O上的一点，过C的直线交直线AB于E，交过A点的切线于D，BC∥OD．
（Ⅰ）求证：DE是圆O的切线；
（Ⅱ）如果AD=AB=2，求EB．
（Ⅰ）证：连接AC，AB是直径，则BC⊥AC
由BC∥OD?OD⊥AC
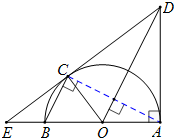
则OD是AC的中垂线?∠OCA=∠OAC，∠DCA=∠DAC，
?∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=∠DAO=90°．
?OC⊥DE，所以DE是圆O的切线．
（Ⅱ） BC∥OD?∠CBA=∠DOA，∠BCA=∠DAO?△ABC∽△AOD
?
=
?BC=
=
=
?
=
?
=
?
=
?BE=
由BC∥OD?OD⊥AC
则OD是AC的中垂线?∠OCA=∠OAC，∠DCA=∠DAC，
?∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=∠DAO=90°．
?OC⊥DE，所以DE是圆O的切线．
（Ⅱ） BC∥OD?∠CBA=∠DOA，∠BCA=∠DAO?△ABC∽△AOD
?
| BC |
| OA |
| AB |
| OD |
| OA?AB |
| OD |
| 1×2 | ||
|
2
| ||
| 5 |
| BC |
| OD |
| 2 |
| 5 |
| BE |
| OE |
| 2 |
| 5 |
| BE |
| OB |
| 2 |
| 3 |
?BE=
| 2 |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
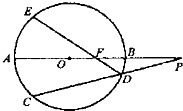（2013•太原一模）选修4一1：几何证明选讲
选修4一1：几何证明选讲
，DE交AB于点F．
