题目内容
如图所示的多面体中, 菱形,
菱形, 是矩形,
是矩形, ⊥平面
⊥平面 ,
, ,
,
 .
.

(Ⅰ)异面直线 与
与 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求证平面 ⊥平面
⊥平面 ;
;
(Ⅲ)在线段 取一点
取一点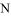 ,当二面角
,当二面角 的大小为60°时,求
的大小为60°时,求 .
.
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
题目内容
如图所示的多面体中, 菱形,
菱形, 是矩形,
是矩形, ⊥平面
⊥平面 ,
, ,
,
 .
.

(Ⅰ)异面直线 与
与 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求证平面 ⊥平面
⊥平面 ;
;
(Ⅲ)在线段 取一点
取一点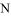 ,当二面角
,当二面角 的大小为60°时,求
的大小为60°时,求 .
.
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案