题目内容
设a、b为正实数．现有下列命题：
①若a2-b2=1，则a-b＜1；
②若|a3-b3|=1，则|a-b|＜1；
③若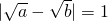
，则|a-b|＜1；
④若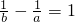
，则a-b＜1．
其中的真命题有________．（写出所有真命题的编号）
①②
分析：由不等式的基本性质和实数的有关理论及因式分解即可判断出是否正确．
解答：①∵a＞0，b＞0，∴a+b＞0，又∵（a-b）（a+b）=1，∴a+b＞1＞a-b＞0，故正确；
②∵a＞0，b＞0，∴a2+ab+b2＞a2-2ab+b2=（a-b）2，
∴1=|a3-b3|=|a-b||a2+ab+b2|＞|a-b|3，∴|a-b|＜1，正确；
③∵|a-b|=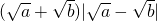
，，∴
＞
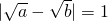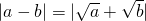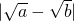=1，故③不正确；
④令a=100，b=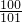
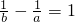，满足，但是a-b＞1，因此不正确．
综上可知：真命题是①②．
故答案为①②．
点评：正确理解不等式的基本性质是解题的关键．
分析：由不等式的基本性质和实数的有关理论及因式分解即可判断出是否正确．
解答：①∵a＞0，b＞0，∴a+b＞0，又∵（a-b）（a+b）=1，∴a+b＞1＞a-b＞0，故正确；
②∵a＞0，b＞0，∴a2+ab+b2＞a2-2ab+b2=（a-b）2，
∴1=|a3-b3|=|a-b||a2+ab+b2|＞|a-b|3，∴|a-b|＜1，正确；
③∵|a-b|=
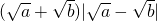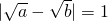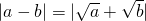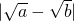，，∴＞=1，故③不正确；④令a=100，b=
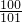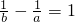，满足，但是a-b＞1，因此不正确．综上可知：真命题是①②．
故答案为①②．
点评：正确理解不等式的基本性质是解题的关键．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为________；最小正周期为________．
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O、O′，现将此三棱柱绕直线OO′旋转（包括逆时针方向和顺时针方向），射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积记为S（x），则函数S（x）的最大值和最小正周期分别是
，
