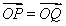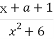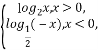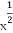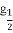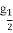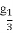题目内容
已知函数f(x)=-x+log2
.
(1)求f(
)+f(-)的值.
(2)当x∈(-a,a],其中a∈(0,1),a是常数时,函数f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,请说明理由.
(1)0 (2) f(x)存在最小值,且为log2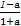
-a
【解析】∵f(x)的定义域为(-1,1),关于原点对称,
(1)f(-x)=x+log2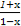
=x-log2
,
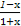∴f(-x)=-f(x),故f(x)在(-1,1)上是奇函数,
因此f(
)+f(-)=f()-f()=0.
(2)∵f(x)=-x+log2(-1+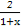
),
令U(x)=-1+,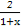
则U(x)在(-1,1)上是减函数,
∴f(x)在(-1,1)上是减函数.
又a∈(0,1),∴当x∈(-a,a]时,f(x)是减函数,
故f(x)min=f(a)=-a+log2,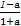
∴f(x)存在最小值,且为log2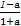-a.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
