Question

【题目】已知函数f（x）=为定义在R上的奇函数．

（1）求a，b的值及f（x）的表达式；

（2）判断f（x）在定义域上的单调性并用单调性的定义证明．

Answer 1

【答案】（1）（2）增函数

【解析】

试题分析：（1）由函数为奇函数可知恒成立，由此带入可求得值，进而得到函数解析式；

（2）证明函数单调性一般采用定义法，首先假设，通过判断的大小关系证明函数单调性

试题解析：（1）∵f（x）=定义在R上的奇函数，

则有f（0）=0，即=0，解可得a=1；………………2分

又f（1）=﹣f（﹣1），即=﹣，解可得b=1．……………4分

∴f（x）=；………………5分

（2）由（1）可得，f（x）=1﹣………………6分

设x1＜x2，………………………………………………7分

则f（x1）﹣f（x2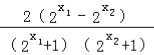）=，………………9分

∵x1＜x2，

∴＜0，………………………………10分

∴f（x1）﹣f（x2）＜0，………………11分

∴f（x）是增函数．………………12分