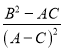Question

【题目】已知椭圆C:1(a>b>0)的左右焦点分别为F1，F2，离心率为，A为椭圆C上一点，且AF2⊥F1F2，且|AF2|.

（1）求椭圆C的方程；

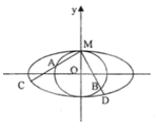
（2）设椭圆C的左右顶点为A1，A2，过A1，A2分别作x轴的垂线 l1，l2，椭圆C的一条切线l:y=kx+m(k≠0)与l1，l2交于M，N两点，试探究是否为定值，并说明理由.

Answer 1

【答案】(1) (2)是，理由见解析

【解析】

（1）设椭圆的焦距为，由已知可得点的横坐标为，将代入椭圆可得，可得，再由离心率，结合，求出，即可求解；

（2）由（1）得l1:x=﹣2，l2:x=2，直线l方程与椭圆方程联立，消去，得到关于的一元二次方程，，求出关系，求出直线l1，l2与直线l的交点坐标，求出，即可求出结论.

(1) 设椭圆的焦距为，根据题意，

A为椭圆C上一点，且AF2⊥F1F2，

点的横坐标为，将代入椭圆可得，

且|AF2|，所以

解得a=2，b，椭圆的方程为：；

(2)由题设知l1:x=﹣2，l2:x=2，直线l:y=kx+m，

联立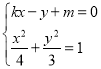，消去y，

得，

故，

l与11，l2联立得M(﹣2，﹣2k+m)，N(2，2k+m)，又F2(1，0)，

所以(3，2k﹣m)(﹣1，﹣2k﹣m)

=﹣3﹣(2k﹣m)(2k+m)=﹣3﹣4k2+m2=0，

故为定值.