题目内容
如图, 与
与 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
, 平面
平面 ,
,

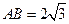 .
.
(1)求直线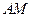 与平面
与平面 所成的角的大小;
所成的角的大小;
(2)求平面 与平面
与平面 所成的二面角的正弦值.
所成的二面角的正弦值.
 与
与 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
, 平面
平面 ,
,
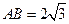 .
.(1)求直线
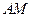 与平面
与平面 所成的角的大小;
所成的角的大小;(2)求平面
 与平面
与平面 所成的二面角的正弦值.
所成的二面角的正弦值.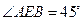 ,
,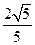
本题主要考查了考查立体图形的空间感、线面角、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
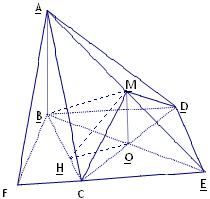
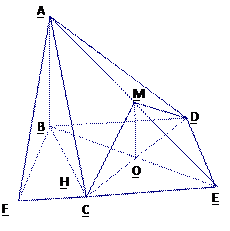
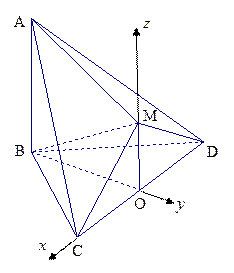
解法一:(1)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD.
又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 ,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
OB=MO=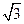 ,MO∥AB,则
,MO∥AB,则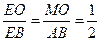 ,
,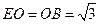 ,所以
,所以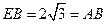 ,故
,故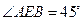 .
.
(2)CE是平面 与平面
与平面 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为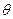 .
.
因为∠BCE=120°,所以∠BCF=60°.
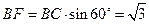 ,
,
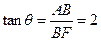 ,
,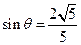
所以,所求二面角的正弦值是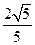 .
.
解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 .
.
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=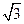 ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,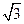 ),B(0,-
),B(0,-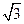 ,0),A(0,-
,0),A(0,-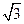 ,2
,2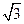 ),
),
(1)设直线AM与平面BCD所成的角为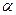 .
.
因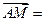 (0,
(0,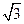 ,
,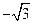 ),平面
),平面 的法向量为
的法向量为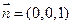 .则有
.则有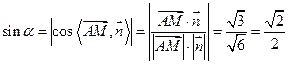 ,所以
,所以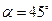 .
.
(2)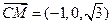 ,
,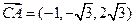 .
.
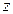 设平面ACM的法向量为
设平面ACM的法向量为 ,由
,由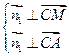 得
得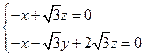 .解得
.解得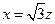 ,
,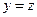 ,取
,取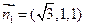 .又平面BCD的法向量为
.又平面BCD的法向量为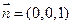 ,则
,则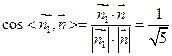
设所求二面角为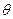 ,则
,则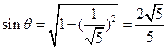 .
.



解法一:(1)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD.
又平面
 平面
平面 ,则MO⊥平面
,则MO⊥平面 ,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.OB=MO=
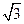 ,MO∥AB,则
,MO∥AB,则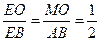 ,
,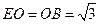 ,所以
,所以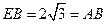 ,故
,故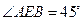 .
.(2)CE是平面
 与平面
与平面 的交线.
的交线.由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为
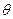 .
.因为∠BCE=120°,所以∠BCF=60°.
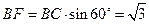 ,
,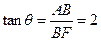 ,
,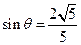
所以,所求二面角的正弦值是
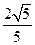 .
.解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面
 平面
平面 ,则MO⊥平面
,则MO⊥平面 .
.以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=
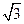 ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,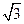 ),B(0,-
),B(0,-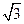 ,0),A(0,-
,0),A(0,-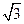 ,2
,2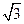 ),
),(1)设直线AM与平面BCD所成的角为
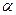 .
.因
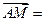 (0,
(0,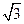 ,
,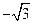 ),平面
),平面 的法向量为
的法向量为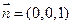 .则有
.则有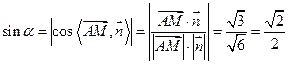 ,所以
,所以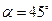 .
.(2)
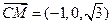 ,
,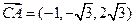 .
.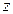 设平面ACM的法向量为
设平面ACM的法向量为 ,由
,由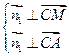 得
得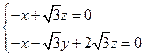 .解得
.解得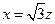 ,
,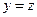 ,取
,取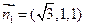 .又平面BCD的法向量为
.又平面BCD的法向量为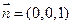 ,则
,则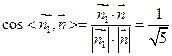
设所求二面角为
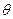 ,则
,则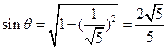 .
.
练习册系列答案
相关题目
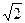 ,BC=
,BC= ,AA1=
,AA1=
 是正方形
是正方形 所在平面外一点,
所在平面外一点, 平面
平面 ,点
,点 、
、 分别在线段
分别在线段 、
、 上,满足
上,满足 .
. 与平面
与平面 ;
;
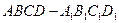 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系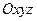 ,
,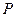 在线段
在线段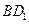 上,且满足
上,且满足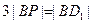 ,试写出点
,试写出点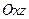 的对称点
的对称点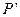 的坐标;
的坐标;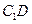 中点为
中点为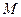 ,求点
,求点 , 四边形
, 四边形 是梯形,
是梯形, ∥
∥ ,
,  ,
, ,
, 

 中
中 点。
点。
 ∥平面
∥平面 ;
; 所成角的余弦值。
所成角的余弦值。
 B.
B. C.
C. D.
D.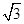

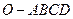 中,
中,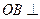 底面
底面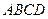 ,且
,且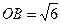 ,底面
,底面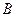 在平面
在平面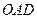 内的射影
内的射影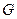 恰为
恰为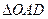 的重心.
的重心.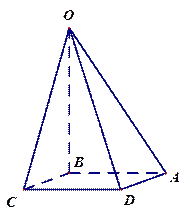 ①求
①求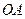 的长;
的长;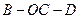 的平面角的余弦值.
的平面角的余弦值. 中,
中, ,
, ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )

