题目内容
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且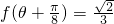 ,求tan2θ的值.
,求tan2θ的值.
(1)解:f(x)=2sinxcosx+cos2x=sin2x+cos2x(2分)
= (3分)
(3分)
=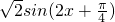 .(4分)
.(4分)
∴f(x)的最小正周期为 ,最大值为
,最大值为 .(6分)
.(6分)
(2)解:∵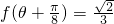 ,∴
,∴ .(7分)
.(7分)
∴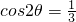 .(8分)
.(8分)
∵θ为锐角,即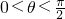 ,∴0<2θ<π.
,∴0<2θ<π.
∴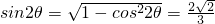 .(10分)
.(10分)
∴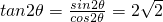 .(12分)
.(12分)
分析:(1)利用二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期和最大值;
(2)通过θ为锐角,且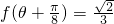 ,求出cos2θ的值,sin2θ的值,然后求tan2θ的值.
,求出cos2θ的值,sin2θ的值,然后求tan2θ的值.
点评:本小题主要考查三角函数性质,同角三角函数的基本关系、两倍角公式等知识,考查化归与转化的数学思想方法和运算求解能力.
=
 (3分)
(3分)=
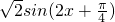 .(4分)
.(4分)∴f(x)的最小正周期为
 ,最大值为
,最大值为 .(6分)
.(6分)(2)解:∵
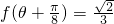 ,∴
,∴ .(7分)
.(7分)∴
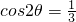 .(8分)
.(8分)∵θ为锐角,即
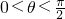 ,∴0<2θ<π.
,∴0<2θ<π.∴
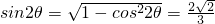 .(10分)
.(10分)∴
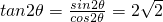 .(12分)
.(12分)分析:(1)利用二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期和最大值;
(2)通过θ为锐角,且
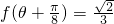 ,求出cos2θ的值,sin2θ的值,然后求tan2θ的值.
,求出cos2θ的值,sin2θ的值,然后求tan2θ的值.点评:本小题主要考查三角函数性质,同角三角函数的基本关系、两倍角公式等知识,考查化归与转化的数学思想方法和运算求解能力.

练习册系列答案
相关题目