Question

统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为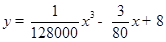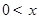：(≤120).已知甲、乙两地相距100千米。

（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

 

Answer 1

【答案】

（1）17.5升；（2）当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升.

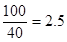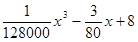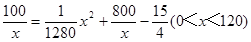【解析】本试题主要考查了导数在研究函数中的运用。第一问，首先表示当x=40时，汽车从甲地到乙地行驶了小时，然后代入已知关系式可知。第二问中，当速度为x千米/小时，汽车从甲地到乙地行驶了耗油量为h(x)升，依题意得h(x)=()·,利用导数判定单调性，进而得到最值。

解: (1)当x=40时，汽车从甲地到乙地行驶了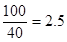小时,

要耗油(.

答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升. 

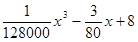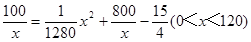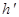(2)当速度为x千米/小时，汽车从甲地到乙地行驶了设耗油量为h(x)升，依题意得h(x)=()·, 

(x)=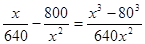    其中0＜x≤120                   

令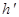(x)=0，得x=80.

当x∈(0,80)时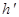，(x)＜0,h(x)是减函数;

当x∈(80,120)时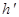，(x)＞0,h(x)是增函数.

∴当x=80时，h(x)取到极小值h(80)=11.25.

因为h(x)在(0,120)上只有一个极值，所以它是最小值.

答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，

最少为11.25升.