题目内容
【题目】已知a>0,函数f(x)= ![]() +|lnx﹣a|,x∈[1,e2].
+|lnx﹣a|,x∈[1,e2].
(1)当a=3时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)若f(x)≤ ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(1)解:当a=3时,f(x)= ![]() +|lnx﹣3|=
+|lnx﹣3|= ![]() ﹣lnx+3,x∈[1,e2];
﹣lnx+3,x∈[1,e2];
故f(3)=1﹣ln3+3=4﹣ln3,
f′(x)=﹣ ![]() ﹣
﹣ ![]() ,f′(3)=﹣
,f′(3)=﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ;
;
故曲线y=f(x)在点(3,f(3))处的切线方程为y﹣(4﹣ln3)=﹣ ![]() (x﹣3),
(x﹣3),
即2x+3y﹣18+3ln3=0
(2)解:由题意得, ![]() +|lnx﹣a|≤
+|lnx﹣a|≤ ![]() ,
,
当a≥2时,上式可化为 ![]() ﹣lnx+a≤
﹣lnx+a≤ ![]() 恒成立,
恒成立,
且 ![]() ﹣lnx+a在[1,e2]上是减函数,
﹣lnx+a在[1,e2]上是减函数,
故只需使a+a≤ ![]() ,无解;
,无解;
当0<a<2时,
f(x)= 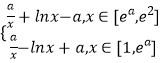 ,
,
故f(x)在[1,ea]上是减函数,在[ea,e2]上是增函数,
故只需使 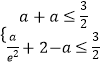 ;
;
解得 ![]() ≤a≤
≤a≤ ![]()
【解析】(1)当a=3时,化简f(x)= ![]() +|lnx﹣3|=
+|lnx﹣3|= ![]() ﹣lnx+3,x∈[1,e2];从而求导,再求切线方程;(2)由题意得,
﹣lnx+3,x∈[1,e2];从而求导,再求切线方程;(2)由题意得, ![]() +|lnx﹣a|≤
+|lnx﹣a|≤ ![]() ,分a≥2与0<a<2讨论求函数的最值,从而化恒成立问题为最值问题即可.
,分a≥2与0<a<2讨论求函数的最值,从而化恒成立问题为最值问题即可.
【考点精析】通过灵活运用函数的最大(小)值与导数,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】在某测试中,卷面满分为100分,60分为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
分数段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人数 | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人数 | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根据上述表格完成列联表:
及格人数 | 不及格人数 | 总计 | |
午休 | |||
不午休 | |||
总计 |
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?

