题目内容
如图，在四棱锥E－ABCD中，AB⊥平面BCE，CD⊥平面BCE，AB=BC=CE=2CD=2，∠BCE=1200．
（I）求证：平面ADE⊥平面ABE ；
（II）求二面角A—EB—D的大小的余弦值．
【答案】
(Ⅰ) 证明略（Ⅱ）二面角A—EB—D的余弦值为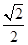
．
【解析】本题综合考查了面面垂直的判定以及二面角的求法和点到面的距离计算．在求点到面的距离时，如果直接法不好求的话，一般转化为棱锥的高利用等体积法来求．
（Ⅰ）取BE的中点O，连OC，OF，DF，可利用条件得OC∥FD，再利用条件证得OC⊥平面ABE即可得到平面ADE⊥平面ABE；
（Ⅱ）因为二面角A-EB-D与二面角F-EB-D相等，即找二面角F-EB-D的平面角为∠FOD即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
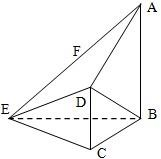如图，在四棱锥E-ABCD中，AB⊥平面BCE，CD⊥平面BCE，AB=BC=CE=2CD=2，∠BCE=120°，F为AE中点．
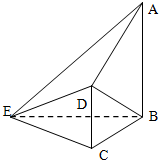如图，在四棱锥E-ABCD中，AB⊥平面BCE，CD⊥平面BCE，AB=BC=CE=2CD=2，∠BCE=120°．
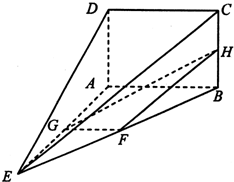（2013•贵阳二模）如图，在四棱锥E-ABCD中，矩形ABCD所在的平面与平面AEB垂直，且∠BAE=120°，AE=AB=4，AD=2，F，G，H分别为BE，AE，BC的中点
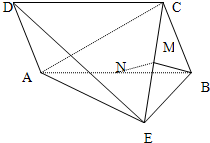（2012•淮南二模）如图，在四棱锥E-ABCD中，四边形ABCD为平行四边形，BE=BC，AE⊥BE，M为CE上一点，且BM⊥面ACE．