题目内容
(本小题16分)
已知函数![]() (
(![]() ).
).
(1)求函数![]() 的值域;
的值域;
(2)①判断函数![]() 的奇偶性;②用定义判断函数
的奇偶性;②用定义判断函数![]() 的单调性;
的单调性;
(3)解不等式![]() .
.
解析:(1)∵ ![]() ,………………………… 2分
,………………………… 2分
又![]() ,∴
,∴![]()
∴函数![]() 的值域为
的值域为![]() ………………………………4分
………………………………4分
(2)证明:①![]() , ………………………6分
, ………………………6分
∴函数![]() 为奇函数 ………………………7分
为奇函数 ………………………7分
② ![]() =
=![]()
在定义域中任取两个实数![]() ,且
,且![]() , …………………………8分
, …………………………8分
则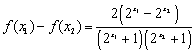 …………………………10分
…………………………10分
![]() ,从而
,从而![]()
![]() …………………………11分
…………………………11分
∴函数![]() 在
在![]() 上为单调增函数 …………………………12分
上为单调增函数 …………………………12分
(3)由(2)得函数![]() 为奇函数,在R上为单调增函数
为奇函数,在R上为单调增函数
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() …………………………14分
…………………………14分
∴原不等式的解集为![]() …………………………16分
…………………………16分

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。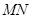 为直径的圆
为直径的圆 经过焦点
经过焦点
 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
. 的值与点
的值与点 的坐标;
的坐标; 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.