题目内容
把正奇数数列 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
………………………
……………………………
设
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数.
(1)若 ,求
,求 的值;
的值;
(2)若记三角形数表中从上往下数第 行各数的和为
行各数的和为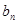 ,求证
,求证 .(本题满分14分)
.(本题满分14分)
【答案】
(1) (2)见解析。
(2)见解析。
【解析】
试题分析:
(1)∵三角形数表中前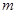 行共有
行共有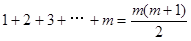 个数,……2分
个数,……2分
∴第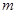 行最后一个数应当是所给奇数列中的第
行最后一个数应当是所给奇数列中的第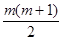 项.
项.
故第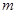 行最后一个数是
行最后一个数是 . ……………………3分
. ……………………3分
因此,使得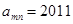 的m是不等式
的m是不等式 的最小正整数解.
的最小正整数解.
由 得
得
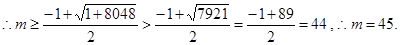 ………………5分
………………5分
于是,第45行第一个数是
 …………………………………………………………6分
…………………………………………………………6分
(2)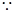 第n行最后一个数是
第n行最后一个数是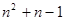 ,且有n个数,若将
,且有n个数,若将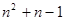 看成第n行第一个数,则第n行各数成公差为
看成第n行第一个数,则第n行各数成公差为 的等差数列,
的等差数列,
故.………………………………………8分
 ,
, …………………10分
…………………10分
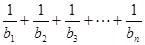
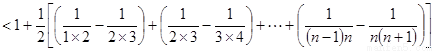 …………12分
…………12分
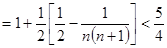 ……………………………………………………………14分
……………………………………………………………14分
考点:本题考查等差数列的前n项和公式、放缩法、裂项法以及分析问题解决问题的能力。
点评:常见的裂项公式: ,
,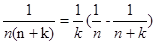 ,
,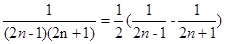 ,
, ,
, ,
,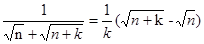

练习册系列答案
相关题目
| |||||||||||


 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数.
个数.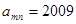 ,求
,求 的值;
的值; 的反函数为
的反函数为 ,
, ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第 行各数的和为
行各数的和为 .
. 的前
的前 .
. 设
设 的前
的前 ,求证:
,求证:
