题目内容
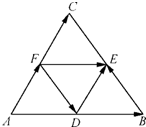（2012•资阳二模）如图，D、E、F分别是△ABC的边AB、BC、CA的中点，则| AF |
| DB |
分析：利用D、E、F分别是△ABC的边AB、BC、CA的中点，及向量的减法三角形法则，可得结论．
解答：解：∵D是△ABC的边AB的中点
∴
=
∴
-
=
-
=
∵D、F分别是△ABC的边AB、CA的中点
∴
=
∵E是△ABC的边BC的中点
∴
=
∴
=
故选D．
∴
| AD |
| DB |
∴
| AF |
| DB |
| AF |
| AD |
| DF |
∵D、F分别是△ABC的边AB、CA的中点
∴
| DF |
| 1 |
| 2 |
| BC |
∵E是△ABC的边BC的中点
∴
| BE |
| 1 |
| 2 |
| BC |
∴
| DF |
| BE |
故选D．
点评：本题考查向量的减法三角形法则，考查共线向量，属于基础题．
练习册系列答案
相关题目
