题目内容
(2012•资阳二模)设函数f(x)=1-e-x,函数g(x)=
(其中a∈R,e是自然对数的底数).
(Ⅰ)当a=0时,求函数h(x)=f'(x)•g(x)的极值;
(Ⅱ)若f(x)≤g(x)在[0,+∞)上恒成立,求实数a的取值范围;
(Ⅲ)设n∈N*,求证:e2n-
≤n!≤e
(其中e是自然对数的底数).
| x |
| ax+1 |
(Ⅰ)当a=0时,求函数h(x)=f'(x)•g(x)的极值;
(Ⅱ)若f(x)≤g(x)在[0,+∞)上恒成立,求实数a的取值范围;
(Ⅲ)设n∈N*,求证:e2n-
| n |
 |
| k=1 |
| 4 |
| k+1 |
| n(n-1) |
| 2 |
分析:(Ⅰ)由f(x)=1-e-x,知f′(x)=-e-x•(-1)=e-x,故函数h(x)=f′(x)•g(x)=xe-x,h′(x)=(1-x)•e-x,由此能求出函数h(x)=f'(x)•g(x)的极值.
(Ⅱ)由题1-e-x≤
在[0,+∞)上恒成立,由x≥0,1-e-x∈[0,1),知
≥0,分类讨论能够得到不等式f(x)≤g(x)在[0,+∞)上恒成立时,实数a的取值范围.
(Ⅲ)由(Ⅱ)知,当a=
时,则1-e-x≤
,故e-x≥
,由此能证明e2n-
≤n!≤e
.
(Ⅱ)由题1-e-x≤
| x |
| ax+1 |
| x |
| ax+1 |
(Ⅲ)由(Ⅱ)知,当a=
| 1 |
| 2 |
| x | ||
|
| 2-x |
| 2+x |
| n |
 |
| k=1 |
| 4 |
| k+1 |
| n(n-1) |
| 2 |
解答:解:(Ⅰ)∵f(x)=1-e-x,∴f′(x)=-e-x•(-1)=e-x,
函数h(x)=f′(x)•g(x)=xe-x,
∴h′(x)=(1-x)•e-x,当x<1时,h′(x)>0;当x>1时,h′(x)<0,
故该函数在(-∞,1)上单调递增,在(1,+∞)上单调递减.
∴函数h(x)在x=1处取得极大值h(1)=
.(4分)
(Ⅱ)由题1-e-x≤
在[0,+∞)上恒成立,
∵x≥0,1-e-x∈[0,1),∴
≥0,
若x=0,则a∈R,若x>0,则a>-
恒成立,则a≥0.
不等式1-e-x≤
恒成立等价于(ax+1)(1-e-x)-x≤0在[0,+∞)上恒成立,(6分)
令μ(x)=(ax+1)(1-e-x),则μ′(x)=a(1-e-x)+(ax+1)e-x-1,
又令v(x)=a(1-e-x)+(ax+1)e-x-1,
则v′(x)=e-x(2a-ax-1),∵x≥0,a≥0.
①当a=0时,v′(x)=-e-x<0,
则v(x)在[0,+∞)上单调递减,∴v(x)=μ′(x)≤v(0)=0,
∴μ(x)在[0,+∞)上单减,∴μ(x)≤μ(0)=0,
即f(x)≤g(x)在[0,+∞)上恒成立;(7分)
②当a≥0时,v′(x)=-a•e-x(x-
).
ⅰ)若2a-1≤0,即0<a≤
时,v′(x)≤0,则v(x)在[0,+∞)上单调递减,
∴v(x)=μ′(x)≤v(0)=0,
∴μ(x)在[0,+∞)上单调递减,
∴μ(x)≤μ(0)=0,
此时f(x)≤g(x)在[0,+∞)上恒成立;(8分)
ⅱ)若2a-1>0,即a>
时,若0<x<
时,
v′(x)>0,则v(x)在(0,
)上单调递增,
∴v(x)=μ′(x)>v(0)=0,∴μ(x)在(0,
)上也单调递增,
∴μ(x)>μ(0)=0,即f(x)>g(x),不满足条件.(9分)
综上,不等式f(x)≤g(x)在[0,+∞)上恒成立时,实数a的取值范围是[0,
].(10分)
(Ⅲ)由(Ⅱ)知,当a=
时,则1-e-x≤
,
∴e-x≥
,
当x∈[0,2)时,e-x≥
,∴x≤ln
,
令
=n,则x=
=2-
,
∴lnn≥2-
(n∈N*),∴
lnk≥2n-
,
∴ln(n!)≥2n-
,(12分)
又由(Ⅰ)得h(x)≤h(1),即xe-x≤
,当x>0时,ln(xe-x)≤ln
=-1,∴lnx≤x-1,
ln(n!)=ln2+ln3+…+lnn≤1+2+…+(n-1)=
,
综上得2n-
≤ln(n!)≤
,
即e2n-
≤n!≤e
.(14分)
函数h(x)=f′(x)•g(x)=xe-x,
∴h′(x)=(1-x)•e-x,当x<1时,h′(x)>0;当x>1时,h′(x)<0,
故该函数在(-∞,1)上单调递增,在(1,+∞)上单调递减.
∴函数h(x)在x=1处取得极大值h(1)=
| 1 |
| e |
(Ⅱ)由题1-e-x≤
| x |
| ax+1 |
∵x≥0,1-e-x∈[0,1),∴
| x |
| ax+1 |
若x=0,则a∈R,若x>0,则a>-
| 1 |
| x |
不等式1-e-x≤
| x |
| ax+1 |
令μ(x)=(ax+1)(1-e-x),则μ′(x)=a(1-e-x)+(ax+1)e-x-1,
又令v(x)=a(1-e-x)+(ax+1)e-x-1,
则v′(x)=e-x(2a-ax-1),∵x≥0,a≥0.
①当a=0时,v′(x)=-e-x<0,
则v(x)在[0,+∞)上单调递减,∴v(x)=μ′(x)≤v(0)=0,
∴μ(x)在[0,+∞)上单减,∴μ(x)≤μ(0)=0,
即f(x)≤g(x)在[0,+∞)上恒成立;(7分)
②当a≥0时,v′(x)=-a•e-x(x-
| 2a-1 |
| a |
ⅰ)若2a-1≤0,即0<a≤
| 1 |
| 2 |
∴v(x)=μ′(x)≤v(0)=0,
∴μ(x)在[0,+∞)上单调递减,
∴μ(x)≤μ(0)=0,
此时f(x)≤g(x)在[0,+∞)上恒成立;(8分)
ⅱ)若2a-1>0,即a>
| 1 |
| 2 |
| 2a-1 |
| a |
v′(x)>0,则v(x)在(0,
| 2a-1 |
| a |
∴v(x)=μ′(x)>v(0)=0,∴μ(x)在(0,
| 2a-1 |
| a |
∴μ(x)>μ(0)=0,即f(x)>g(x),不满足条件.(9分)
综上,不等式f(x)≤g(x)在[0,+∞)上恒成立时,实数a的取值范围是[0,
| 1 |
| 2 |
(Ⅲ)由(Ⅱ)知,当a=
| 1 |
| 2 |
| x | ||
|
∴e-x≥
| 2-x |
| 2+x |
当x∈[0,2)时,e-x≥
| 2-x |
| 2+x |
| 2+x |
| 2-x |
令
| 2+x |
| 2-x |
| 2n-2 |
| n+1 |
| 4 |
| n+1 |
∴lnn≥2-
| 4 |
| n+1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| 4 |
| k+1 |
∴ln(n!)≥2n-
| n |
 |
| k=1 |
| 4 |
| k+1 |
又由(Ⅰ)得h(x)≤h(1),即xe-x≤
| 1 |
| e |
| 1 |
| e |
ln(n!)=ln2+ln3+…+lnn≤1+2+…+(n-1)=
| n(n-1) |
| 2 |
综上得2n-
| n |
 |
| k=1 |
| 4 |
| k+1 |
| n2-n |
| 2 |
即e2n-
| n |
 |
| k=1 |
| 4 |
| k+1 |
| n(n-1) |
| 2 |
点评:本题考查函数极值的求法,求实数的取值范围,证明不等式.考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
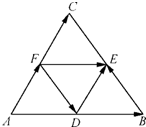 (2012•资阳二模)如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则
(2012•资阳二模)如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则