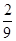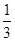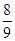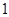题目内容
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为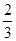 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为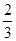 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
(1)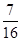 (2)
(2)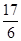 (3)
(3)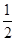
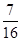 (2)
(2)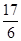 (3)
(3)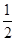
(1)记:“该射手恰好命中两次”为事件A,“该射手第一次射击甲靶命中”为事件B,“该射手第二次射击甲靶命中”为事件C,“该射手射击乙靶命中”为事件D.
由题意知,P(B)=P(C)= ,P(D)=
,P(D)=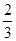 ,所以P(A)=P(BC
,所以P(A)=P(BC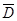 )+P(B
)+P(B D)+P(
D)+P(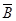 CD)=P(B)P(C)P(
CD)=P(B)P(C)P(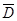 )+P(B)P(
)+P(B)P( )P(D)+P(
)P(D)+P(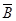 )P(C)P(D)=
)P(C)P(D)= ×
× ×
×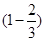 +
+ ×
× ×
×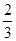 +
+ ×
× ×
×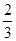 =
=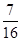 .
.
(2)根据题意,X的所有可能取值为0,1,2,3,4.P(X=0)=P(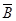

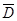 )=
)= ×
× ×
×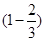 =
=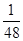 ;
;
P(X=1)=P(B
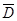 )+P(
)+P(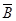 C
C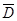 )=
)= ×
× ×
×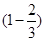 +
+ ×
× ×
×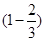 =
=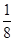 ;
;
P(X=2)=P(BC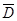 )+P(
)+P(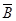
 D)=
D)= ×
× ×
×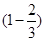 +
+ ×
× ×
×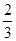 =
=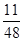 ;
;
P(X=3)=P(B D)+P(
D)+P(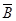 CD)=
CD)= ×
× ×
×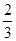 +
+ ×
× ×
×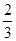 =
=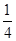 ;
;
P(X=4)=P(BCD)= ×
× ×
×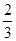 =
=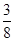 .
.
故X的分布列为
所以E(X)=0×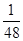 +1×
+1×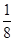 +2×
+2×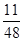 +3×
+3×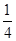 +4×
+4×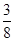 =
=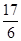 .
.
(3)设“该射手向甲靶射击比向乙靶射击多击中一次”为事件A1,“该射手向甲靶射击命中一次且向乙靶射击未命中”为事件B1,“该射手向甲靶射击命中2次且向乙靶射击命中”为事件B2,则A1=B1∪B2,B1,B2为互斥事件.
P(A1)=P(B1)+P(B2)= ×
× ×
×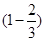 +
+ ×
× ×
×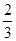 =
=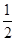 .
.
所以,该射手向甲靶射击比向乙靶射击多击中一次的概率为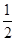 .
.
由题意知,P(B)=P(C)=
 ,P(D)=
,P(D)=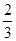 ,所以P(A)=P(BC
,所以P(A)=P(BC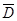 )+P(B
)+P(B D)+P(
D)+P(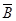 CD)=P(B)P(C)P(
CD)=P(B)P(C)P(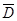 )+P(B)P(
)+P(B)P( )P(D)+P(
)P(D)+P(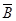 )P(C)P(D)=
)P(C)P(D)= ×
× ×
×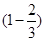 +
+ ×
× ×
×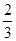 +
+ ×
× ×
×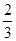 =
=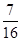 .
.(2)根据题意,X的所有可能取值为0,1,2,3,4.P(X=0)=P(
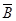

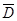 )=
)= ×
× ×
×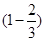 =
=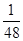 ;
;P(X=1)=P(B

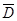 )+P(
)+P(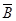 C
C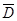 )=
)= ×
× ×
×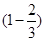 +
+ ×
× ×
×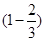 =
=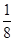 ;
;P(X=2)=P(BC
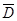 )+P(
)+P(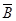
 D)=
D)= ×
× ×
×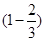 +
+ ×
× ×
×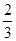 =
=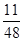 ;
;P(X=3)=P(B
 D)+P(
D)+P(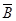 CD)=
CD)= ×
× ×
×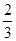 +
+ ×
× ×
×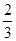 =
=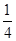 ;
;P(X=4)=P(BCD)=
 ×
× ×
×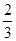 =
=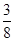 .
.故X的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | 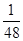 | 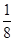 | 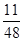 | 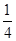 | 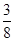 |
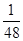 +1×
+1×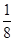 +2×
+2×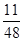 +3×
+3×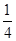 +4×
+4×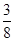 =
=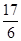 .
.(3)设“该射手向甲靶射击比向乙靶射击多击中一次”为事件A1,“该射手向甲靶射击命中一次且向乙靶射击未命中”为事件B1,“该射手向甲靶射击命中2次且向乙靶射击命中”为事件B2,则A1=B1∪B2,B1,B2为互斥事件.
P(A1)=P(B1)+P(B2)=
 ×
× ×
×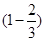 +
+ ×
× ×
×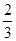 =
=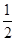 .
.所以,该射手向甲靶射击比向乙靶射击多击中一次的概率为
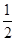 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

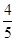



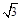 ]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )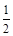
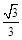
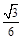
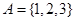 ,
,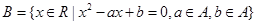 ,则
,则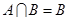 的概率是
的概率是