题目内容
11.已知函数f(x)=ex,x∈R.(1)若直线y=kx与f(x)的反函数的图象相切,求实数k的值;
(2)若m<0,讨论函数g(x)=f(x)+mx2零点的个数.
分析 (1)先求出f(x)的反函数,设出切点的坐标,从而求出k的值;(2)问题掌握求函数f(x)=ex和h(x)=-mx2的交点问题,画出图象读出即可.
解答 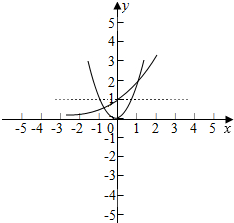 解:(1)函数f(x)=ex的反函数为y=lnx,${y}^{′}=\frac{1}{x}$,
解:(1)函数f(x)=ex的反函数为y=lnx,${y}^{′}=\frac{1}{x}$,
设直线y=kx与f(x)的反函数的图象相切于点P(x0,lnx0),
∴$k=\frac{1}{{x}_{0}}$,lnx0=kx0,
解得x0=e,k=$\frac{1}{e}$;
(2)令g(x)=f(x)+mx2=ex+mx2=0,
得:ex=-mx2,∵m<0,∴-m>0,
画出函数f(x)=ex和h(x)=-mx2,如图示:
∴函数g(x)有2个零点.
点评 本题考查了利用导数研究函数的单调性极值零点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目