题目内容
2.已知函数$f(x)=\left\{\begin{array}{l}{2^x},x≤2\\ f(x-1),x>2\end{array}\right.$,则$f(\frac{9}{2})$=2$\sqrt{2}$.分析 由已知条件利用分段函数的性质求解.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}{2^x},x≤2\\ f(x-1),x>2\end{array}\right.$,
∴$f(\frac{9}{2})$=f($\frac{7}{2}$)=f($\frac{5}{2}$)=f($\frac{3}{2}$)=${2}^{\frac{3}{2}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查函数值的求法,是基础题,解题时要注意分段函数的性质的合理运用.

练习册系列答案
相关题目
10.{an}是首顶a1=1,公差d=3的等差数列,如果an=265,则序号n等于( )
| A. | 91 | B. | 90 | C. | 89 | D. | 88 |
17.设f(x)=2x+3x-8,则方程f(x)=0的根落在区间( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
14.设集合A={x|x>-1},则( )
| A. | ∅∈A | B. | 0∈A | C. | -1∈A | D. | {-1}⊆A |
 在正方体ABCD-A1B1C1D1中.
在正方体ABCD-A1B1C1D1中.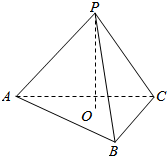 如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.
如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.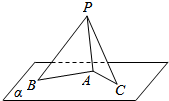 如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:
如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求: