题目内容
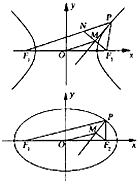 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(0,c)
(0,c)
.分析:类比双曲线中的研究方法,结合椭圆的定义,即可确定|OM|的取值范围.
解答:解:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
|NF1|=
(|PF1|-|PF2|)
∵|PF1|+|PF2|=2a
∴|OM|=a-|PF2|
∵a-c≤|PF2|≤a+c
∵P、F1、F2三点不共线
∴0<a-|PF2|<c
∴0<|OM|<c
故答案为:(0,c).
| 1 |
| 2 |
| 1 |
| 2 |
∵|PF1|+|PF2|=2a
∴|OM|=a-|PF2|
∵a-c≤|PF2|≤a+c
∵P、F1、F2三点不共线
∴0<a-|PF2|<c
∴0<|OM|<c
故答案为:(0,c).
点评:本题考查类比推理,考查椭圆的定义,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
 已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,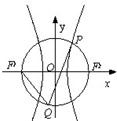 如图,点P是双曲线C1:
如图,点P是双曲线C1:
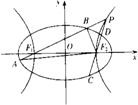 如图,已知椭圆
如图,已知椭圆 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: