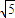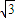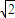题目内容
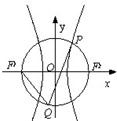 如图,点P是双曲线C1:
如图,点P是双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
分析:由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,根据此直角三角形,结合双曲线的离心率的定义即可求得双曲线C1的离心率
+1.
| 3 |
解答: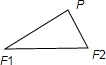 解:由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,
解:由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,
∵在此直角三角形中,∠P=90°,∠F2=60°
∴双曲线C1的离心率=
=
+1,
故填:
+1.
 解:由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,
解:由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,∵在此直角三角形中,∠P=90°,∠F2=60°
∴双曲线C1的离心率=
| PF1+PF2 |
| F1F2 |
| 3 |
故填:
| 3 |
点评:灵活巧妙地运用双曲线的比值定义于解题中,将会带给我们意想不到的方便和简单.应着重培养学生灵活运用知识的能力.结合双曲线的离心率的定义即可求得双曲线C1的离心率.

练习册系列答案
相关题目
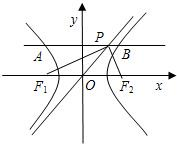 我们定义双曲线C:
我们定义双曲线C: (2013•婺城区模拟)已知点P是双曲线C:
(2013•婺城区模拟)已知点P是双曲线C: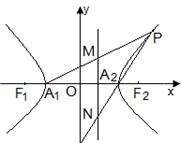
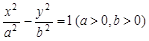 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )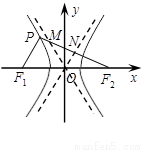
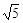 B.2 C.
B.2 C.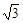 D.
D.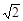
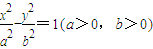 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )