题目内容
【题目】函数![]() 的一段图象如图所示.
的一段图象如图所示.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象,求直线
的图象,求直线![]() 与
与
函数![]() 的图象在
的图象在![]() 内所有交点的坐标.
内所有交点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)依据题设中提供的函数图像,分析探求出函数解析式中的参数的值;(2)借助题设条件建立方程组分析探求:
(1)由图知A=2,T=π,于是ω=![]() =2,
=2,
将y=2sin 2x的图象向左平移![]() ,得y=2sin(2x+φ)的图象.
,得y=2sin(2x+φ)的图象.
于是φ=2·![]() =
=![]() ,
,
∴f(x)=2sin![]() .
.
(2)依题意得
g(x)=2sin![]() =2sin
=2sin![]() . 故y=
. 故y=![]() g(x)=2
g(x)=2![]() sin
sin![]() . 由
. 由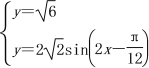 得sin
得sin![]() =
=![]() .
.
∴2x-![]() =
=![]() +2kπ或2x-
+2kπ或2x-![]() =
=![]() +2kπ(k∈Z),
+2kπ(k∈Z),
∴x=![]() +kπ或x=
+kπ或x=![]() +kπ(k∈Z). ∵x∈(0,π),
+kπ(k∈Z). ∵x∈(0,π),
∴x=![]() 或x=
或x=![]() . ∴交点坐标为
. ∴交点坐标为![]() ,
,![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
分 组 | 频 数 | 频 率 |
[-3,-2) | 0.10 | |
[-2,-1) | 8 | |
(1,2] | 0.50 | |
(2,3] | 10 | |
(3,4] | ||
合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填充完整.
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率.
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.



