题目内容
附加题:(本小题10分,实验班同学必做,其他班学生选做)
是否存在常数a,使得函数f (x)=sin2x+acosx+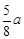 -
-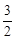 在闭区间
在闭区间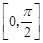 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
【答案】
存在a=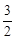 使得f (x)在闭区间
使得f (x)在闭区间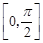 上的最大值为1
上的最大值为1
【解析】解:f (x)=sin2x+acosx+ -
-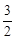
=1-cos2x+acosx+ -
-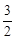 =-cos2x+acosx+
=-cos2x+acosx+ -
-
=-(cosx- a)2+
a)2+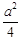 +
+ -
-
∵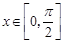 ,∴0≤cosx≤1,
………………1分
,∴0≤cosx≤1,
………………1分
①
若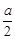 >1,即a>2,则当cosx=1时,f (x)取得最大值,
>1,即a>2,则当cosx=1时,f (x)取得最大值,
f (x)最大值=-(1- a)2+
a)2+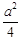 +
+ -
- =
=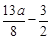 ……………3分
……………3分
令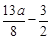 =1,解得
=1,解得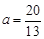 <2(舍去)
……………4分
<2(舍去)
……………4分
②若0≤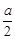 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=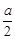 时,f (x)取得最大值,
时,f (x)取得最大值,
f (x)最大值=-( a-
a- a)2+
a)2+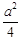 +
+ -
- =
=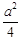 +
+ -
- ……………6分
……………6分
令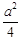 +
+ -
- =1,解得
=1,解得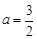 或
或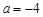 <0(舍去)
……………7分
<0(舍去)
……………7分
③若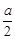 <0,即a<0,则当cosx=0时,f (x)取得最大值,
<0,即a<0,则当cosx=0时,f (x)取得最大值,
f (x)最大值=-(0- a)2+
a)2+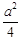 +
+ -
- =
= -
- ……………8分
……………8分
令 -
- =1,解得
=1,解得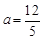 >0(舍去)
……………9分
>0(舍去)
……………9分
综上,存在a=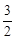 使得f (x)在闭区间
使得f (x)在闭区间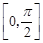 上的最大值为1
……………10分
上的最大值为1
……………10分

练习册系列答案
相关题目
 ,
,
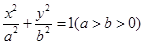 的离心率
的离心率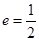 ,且原点
,且原点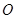 到直线
到直线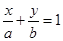 的距离为
的距离为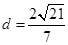 .
.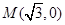 作直线与椭圆C交于
作直线与椭圆C交于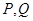 两点,求
两点,求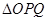 面积的最大值.
面积的最大值.