题目内容
已知A(1,0),B(4,0),动点T(x,y)满足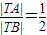 ,设动点T的轨迹是曲线C,直线l:y=kx+1与曲线C交于P,Q两点.
,设动点T的轨迹是曲线C,直线l:y=kx+1与曲线C交于P,Q两点.(1)求曲线C的方程;
(2)若
 ,求实数k的值;
,求实数k的值;(3)过点(0,1)作直线l1与l垂直,且直线l1与曲线C交于M,N两点,求四边形PMQN面积的最大值.
【答案】分析:(1)设D(x,y)为曲线C上任一点,由动点T(x,y)满足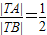 ,利用两点间距离公式能求出曲线C的方程.
,利用两点间距离公式能求出曲线C的方程.
(2)因为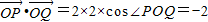 ,所以
,所以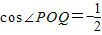 ,∠POQ=120°,由此利用圆心到直线l:kx-y+1=0的距离能求出k.
,∠POQ=120°,由此利用圆心到直线l:kx-y+1=0的距离能求出k.
(3)当k=0时,四边形PMQN面积为4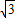 .当k≠0时,圆心到直线l:kx-y+1=0的距离
.当k≠0时,圆心到直线l:kx-y+1=0的距离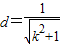 ,SPMQN=
,SPMQN= =2
=2 •
•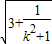 ,由此能求出四边形PMQN面积最大值.
,由此能求出四边形PMQN面积最大值.
解答:解:(1)设D(x,y)为曲线C上任一点,
∵动点T(x,y)满足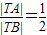 ,
,
∴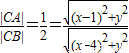 ,
,
化简整理得x2+y2=4.
∴曲线C的方程为x2+y2=4.(3分)
(2)因为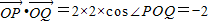 ,
,
所以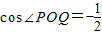 ,∠POQ=120°,
,∠POQ=120°,
所以圆心到直线l:kx-y+1=0的距离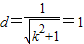 ,
,
所以k=0.(6分)
(3)当k=0时,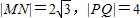 ,
,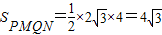
当k≠0时,圆心到直线l:kx-y+1=0的距离 ,
,
所以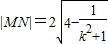
 ,
,
同理得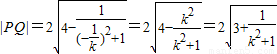 ,
,
∴SPMQN= =2
=2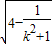 •
•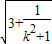 ,
,
S=2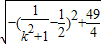 ≤2×
≤2× =7,
=7,
当且仅当k=±1时取等号,
∴当k=±1时,Smax=7,
综上所述,当k=±1时,四边形PMQN面积有最大值7.
点评:本题考查曲线方程的求法,考查满足条件的实数值的求法,考查四边形面积的最大值的求法,解题时要认真审题,注意向量知识、两点间距离公式、点到直线的距离公式等知识点的合理运用.
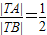 ,利用两点间距离公式能求出曲线C的方程.
,利用两点间距离公式能求出曲线C的方程.(2)因为
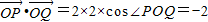 ,所以
,所以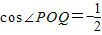 ,∠POQ=120°,由此利用圆心到直线l:kx-y+1=0的距离能求出k.
,∠POQ=120°,由此利用圆心到直线l:kx-y+1=0的距离能求出k.(3)当k=0时,四边形PMQN面积为4
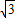 .当k≠0时,圆心到直线l:kx-y+1=0的距离
.当k≠0时,圆心到直线l:kx-y+1=0的距离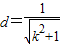 ,SPMQN=
,SPMQN= =2
=2 •
•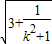 ,由此能求出四边形PMQN面积最大值.
,由此能求出四边形PMQN面积最大值.解答:解:(1)设D(x,y)为曲线C上任一点,
∵动点T(x,y)满足
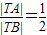 ,
,∴
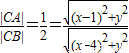 ,
,化简整理得x2+y2=4.
∴曲线C的方程为x2+y2=4.(3分)
(2)因为
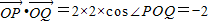 ,
,所以
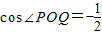 ,∠POQ=120°,
,∠POQ=120°,所以圆心到直线l:kx-y+1=0的距离
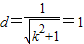 ,
,所以k=0.(6分)
(3)当k=0时,
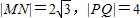 ,
,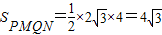
当k≠0时,圆心到直线l:kx-y+1=0的距离
 ,
,所以
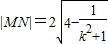
 ,
,同理得
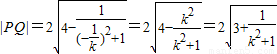 ,
,∴SPMQN=
 =2
=2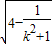 •
•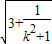 ,
,S=2
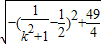 ≤2×
≤2× =7,
=7,当且仅当k=±1时取等号,
∴当k=±1时,Smax=7,
综上所述,当k=±1时,四边形PMQN面积有最大值7.
点评:本题考查曲线方程的求法,考查满足条件的实数值的求法,考查四边形面积的最大值的求法,解题时要认真审题,注意向量知识、两点间距离公式、点到直线的距离公式等知识点的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目