题目内容
已知暗箱中开始有3个红球,2个白球.现每次从暗箱中取出1个球后,再将此球和它同色的另外5个球一起放回箱中.(I)求第2次取出白球的概率;
(Ⅱ)若取出白球得2分,取出红球得3分,设连续取球2次的得分值为X,求X的分布列和数学期望.
【答案】分析:(I)第2次取出白球的事件包括:“第1次取出红球第二次取出白球”、“两次均取出白球”,且互斥,由此可求第2次取出白球的概率;
(Ⅱ)确定X的取值,计算其概率,从而可得X的分布列和数学期望.
解答:解:(I)第2次取出白球的事件包括:“第1次取出红球第二次取出白球”记为事件A,“两次均取出白球”记为事件B,则A,B互斥,所以第2次取出白球的概率为P=P(A)+P(B)=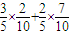 =
=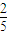 ;
;
(Ⅱ)X的所有可能取值为4,5,6
P(X=4)=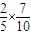 =
=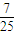 ;P(X=5)=
;P(X=5)=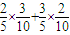 =
=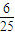 ;P(X=6)=
;P(X=6)=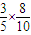 =
=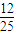
∴X的分布列如下:
∴EX=4× +5×
+5×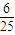 +6×
+6×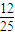 =
=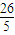 .
.
点评:本题考查概率的性质和应用,解题时要注意离散型随机变量的分布列和期望的应用,合理地运用等可能事件的知识进行解题.
(Ⅱ)确定X的取值,计算其概率,从而可得X的分布列和数学期望.
解答:解:(I)第2次取出白球的事件包括:“第1次取出红球第二次取出白球”记为事件A,“两次均取出白球”记为事件B,则A,B互斥,所以第2次取出白球的概率为P=P(A)+P(B)=
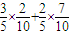 =
=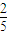 ;
;(Ⅱ)X的所有可能取值为4,5,6
P(X=4)=
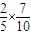 =
=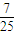 ;P(X=5)=
;P(X=5)=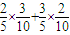 =
=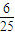 ;P(X=6)=
;P(X=6)=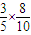 =
=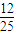
∴X的分布列如下:
| X | 4 | 5 | 6 |
| P | 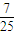 | 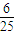 | 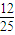 |
 +5×
+5×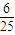 +6×
+6×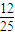 =
=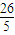 .
.点评:本题考查概率的性质和应用,解题时要注意离散型随机变量的分布列和期望的应用,合理地运用等可能事件的知识进行解题.

练习册系列答案
相关题目